SCF Estimate Quality: The Resolution Product

What factors influence the quality of a spectral correlation function estimate?

The two non-parametric spectral-correlation estimators we’ve looked at so far–the frequency-smoothing and time-smoothing methods–require the choice of key estimator parameters. These are the total duration of the processed data block, $T$ , and the spectral resolution $F$ .

For the frequency-smoothing method (FSM), an FFT with length equal to the data-block length $T$ is required, and the spectral resolution is equal to the width $F$ of the smoothing function $g(f)$ . For the time-smoothing method (TSM), multiple FFTs with lengths $T_{tsm} = T / K$ are required, and the frequency resolution is $1/T_{tsm}$ (in normalized frequency units).

The choice for the block length $T$ is partially guided by practical concerns, such as computational cost and whether the signal is persistent or transient in nature, and partially by the desire to obtain a reliable (low-variance) spectral correlation estimate. The choice for the frequency (spectral) resolution is typically guided by the desire for a reliable estimate.

The reliability of the estimate is inversely proportional to the time-bandwidth product $TF$ . Note that this is the time-bandwidth product of the measurement, not of the signal(s) in the data. This result has been established in [R1] (see Chapter 15, Eq (87a)). In that work, the coefficient of variation of a point estimate of the spectral correlation function is shown to be inversely proportional to the time-bandwidth product

$\displaystyle C_v \approx \displaystyle \frac{C_0}{T F |C_x^\alpha(f)|^2}, \hfill (1)$

where $C_0$ is a constant and the spectral correlation estimate is for frequency $f$ and cycle frequency $\alpha$ . Here the function $C_x^\alpha(f)$ is the spectral coherence for the data $x(t)$ at spectral frequency $f$ and cycle frequency $\alpha$ .

The (non-conjugate) coherence is defined by

$\displaystyle C_x^\alpha (f) = \frac{S_x^\alpha(f)}{\left[ S_x^0(f+\alpha/2) S_x^0(f-\alpha/2) \right]^{1/2}} \hfill (2)$

where $S_x^0(f)$ is the PSD. When $x(t) = s(t) + n(t)$ , we have

$\displaystyle S_x^0(f) = S_s^0(f) + S_n^0(f), \hfill (3)$

and when $n(t)$ is white Gaussian noise, $S_n^0(f) = N_0$ , the noise spectral density value. Moreover, for $\alpha \neq 0$ ,

$\displaystyle S_x^\alpha(f) = S_s^\alpha(f). \hfill (4)$

Suppose $S_s^0(f) \ll N_0$ . Then $S_x^0(f) \approx N_0$ and

$\displaystyle C_v \approx \frac{C_0}{T F | S_s^\alpha(f) / N_0 |^2} \hfill \alpha \neq 0. \hfill (5)$

So the coefficient of variation is also inversely proportional to the square of an SNR measure. As this SNR decreases, the coefficient of variation increases. To regain a smaller coefficient of variation, the resolution product must then be increased.

A simpler result for $\alpha=0$ is well-known in the spectrum analysis community. For example, reference [R43] asserts that the coefficient of variation for a power spectrum estimate (spectral frequency $f$ , cycle frequency $\alpha=0$ ) is inversely proportional to $TF$ (see Section 5.4).

Interpretation

These basic approximate results tell us that if we want to improve the reliability (reduce the variance) of a measurement, we need to increase the data-block length, increase the spectral resolution (make it coarser), or both. It also tells us that we cannot simultaneously have very fine spectral resolution (small $F$ ) and low estimate variability (small $C_v$ ) unless the block length $T$ is made very large.

Numerical Examples

As an illustration, we consider the rectangular-pulse BPSK signal (of course). First we produce a sequence of FSM spectral correlation estimates for only those cycle frequencies exhibited by the signal. The block length is fixed at $32,768$ samples. The resolution product is varied by varying the width of the rectangular spectral smoothing window $g(f)$ . The spectral correlation estimates are plotted as surfaces above the $f-\alpha$ plane and collected in a movie:

Video 1. Successive estimates of the spectral correlation function for rectangular-pulse BPSK. The processing time is fixed at $32768$ samples and the resolution product is varied by changing the width of the smoothing window in the FSM.

When the resolution product is small, the spectral correlation features are difficult to make out due to their highly erratic appearance. As the product increases, the features begin to look like the ideal ones. However, as it continues to increase, the spectral resolution of the measurement becomes larger than the spectral widths of the features (peaks and valleys) in the spectral correlation function, causing the features to become smeared in appearance. At this extreme of the resolution product, the estimates are highly reliable (low variance) but are deterministically distorted (high bias).

The reliability of the spectral correlation estimate is especially important when the cycle frequencies of interest are not known in advance of estimation. In such a case, a cycle-frequency search must be performed. The FSM and TSM are not particularly efficient for this purpose (we will cover an efficient method, the strip spectral correlation analyzer, in a future post), but they are sufficient to illustrate the resolution product effect here.

The FSM was used to estimate the spectral correlation and spectral coherence functions for each unique cycle frequency in the principal domain $[-1.0, 1.0)$ using a block length $T$ of $32,768$ samples and various spectral resolution widths $F$ . The cycle-frequency resolution of a spectral correlation measurement is approximately the reciprocal of the block length $\Delta\alpha \approx 1/T$ . So the set of visited cycle frequencies has adjacent-cycle-frequency spacing of $1/T = 1/32,768$ . That’s a lot of cycle frequencies. The resulting sequence of spectral correlation estimate magnitudes is shown in the following movie:

Perhaps even more important is the spectral coherence, which is a more useful detection statistic than is the spectral correlation. Here is the effect of increasing resolution product on the FSM-based coherence estimates:

Video 3. Successive estimates of the maximum spectral coherence magnitude for a BPSK signal in noise. These are the peak coherence values corresponding to the spectral correlation estimates obtained making Video 2.

My rules of thumb for choosing the block length $T$ and the spectral resolution $F$ are to use as large a $T$ as possible, considering computational cost and whether the signal(s) in the data persist, and a large $F$ when performing a blind search for cycle frequencies. When the cycle frequencies are known in advance, use large $T$ , but choose the spectral resolution $F$ so that the features in the spectral correlation (and PSD) are adequately resolved, but are not over-smoothed.

For the TSM and FSM, good default values for $F$ lie in the range of 1-5% of the sampling frequency for the input data to be analyzed. For the FSM, this means a smoothing window with width (number of frequency bins) equal to about $T/100$ to $T/20$ . For the TSM, this means a FFT block length of about $T_{tsm} = T/128$ to $T/16$ .

Author: Chad Spooner

I'm a signal processing researcher specializing in cyclostationary signal processing (CSP) for communication signals. I hope to use this blog to help others with their cyclo-projects and to learn more about how CSP is being used and extended worldwide. View all posts by Chad Spooner

7 thoughts on “SCF Estimate Quality: The Resolution Product”

Hari prasad says:

December 20, 2019 at 10:35 pm

Hi sir ,please clarify my basic doubts written below
After going through your blog for last few days, I understood in cyclostationary processing ,we are dealing with three dimensional (frequencies per cyclic frequencies ,cyclic frequencies(alpha) and correlation amplitudes).power spectrum density is nothing but spectral correlation function with cyclic frequencies equal to zero.
I would like to ask u what is the interpretation that if whole frequency band(-fs/2 to fs/2 ) present for particular alpha which is not equal to zero,In practical are we interested only cyclic frequencies irrespective of correlation amplitudes present on one frequency or whole band for that particular alpha.

my second doubt is
In this post spectral resolution is nothing but resolution in frequency band (-fs/2 to fs/2)per cyclic frequency, Is my understanding is correct? If so than what about cyclic frequency resolution?

So please clarify my doubts

Reply
1. Chad Spooner says:
  
  December 21, 2019 at 3:12 pm
  
  I would like to ask u what is the interpretation that if whole frequency band(-fs/2 to fs/2 ) present for particular alpha which is not equal to zero,In practical are we interested only cyclic frequencies irrespective of correlation amplitudes present on one frequency or whole band for that particular alpha.
  
  I can’t understand this question. If you can post a clarification, I might be able to answer.
  
  In this post spectral resolution is nothing but resolution in frequency band (-fs/2 to fs/2)per cyclic frequency, Is my understanding is correct? If so than what about cyclic frequency resolution?
  
  I discuss, in detail, temporal, spectral, and cycle-frequency resolution in the post on resolutions in CSP. Take a look and post a comment again if there are still parts that are unclear to you.
  
  Reply
  1. Hari prasad says:
    
    December 22, 2019 at 8:52 pm
    
    Thanks for reply sir
    For that first question, i try to elaborate bit more to get better understanding of my doubt.
    
    I mean spectral density is some correlation amplitude of (alpha and f) ,Sc(alpha,f) ,with that i start asking my doubts
    
    In SCF, for each cyclic frequency(alpha) there is a spectral density ,let say for alpha = 0 ,Sc(f) is power spectral density covers from(-fs/2 to fs/2) , similarly for alpha != 0 ,there may be a spectral density (-fs/2 to fs/2) presents ,if any hidden periodicity presents in the signal(cyclostationary signal).
    
    My question is for alpha not equal to zero , if spectral density presents i.e it may be a peak at particular frequency ,group of frequencies are present from (-fs/2 to fs/2) , what is the interpretation of occuring one peak at particular frequency or band of frequencies for particular alpha != 0 ?
    
    2) In practical , are we interested only on cycle frequencies where spectral density is present(either one particular frequency present or band of freq) or spectral density of that alpha or both?
    
    To be precise , if my baseband signal contains frequency offset, for some alpha != 0 there may be spectral density present , now will it present in one single frequency or entire band (-fs/2 to fs/2).
    
    Reply
    1. Chad Spooner says:
      
      December 23, 2019 at 9:51 am
      
      My question is for alpha not equal to zero , if spectral density presents i.e it may be a peak at particular frequency ,group of frequencies are present from (-fs/2 to fs/2) , what is the interpretation of occuring one peak at particular frequency or band of frequencies for particular alpha != 0 ?
      
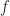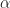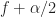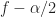      The interpretation of non-zero spectral correlation (non-conjugate) for a particular frequency $f$ and cycle frequency $\alpha$ is that the two time-series corresponding to the narrowband spectral components of the signal with frequencies $f+\alpha/2$ and $f-\alpha/2$ exhibit non-zero correlation coefficient. That is, those two narrowband time series contain some redundant information (or, in the case of a correlation coefficient of one, they contain exactly the same information). This interpretation applies to each 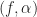$(f, \alpha)$ , and so can be applied to the case of a spectral correlation function that is non-zero only for a single 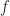$f$ or to one that is non-zero for a range of $f$ .
      
      In practical , are we interested only on cycle frequencies where spectral density is present(either one particular frequency present or band of freq) or spectral density of that alpha or both?
      
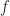      I am interested in cycle frequencies for which the spectral correlation function is not zero for all frequencies. Cycle frequencies for which the spectral correlation function is identically zero (zero for all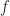 $f$ ) are not particularly interesting unless, I suppose, you happened to be expecting spectral correlation for that cycle frequency and yet it is not present when you test for it.
      
      I don’t understand the phrase “spectral density of that alpha.”
      
      To be precise , if my baseband signal contains frequency offset, for some alpha != 0 there may be spectral density present , now will it present in one single frequency or entire band (-fs/2 to fs/2).
      
      Well, I don’t know of any signal that produces a non-conjugate spectral correlation function that is non-zero only for a single frequency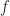 $f$ except for the case of a complex-valued sine wave, which produces an impulse in the PSD.
      
      All of the spectral correlation functions in the Gallery post correspond to baseband signals that have a small carrier frequency offset. I suggest you study those plots.
      
      Reply
Hari prasad says:

December 23, 2019 at 4:58 am

If some hidden periodicity present in the signal like (frequency offset or some header) in that signal which repeats periodically. obviously cyclic frequency is present for alpha!= 0 , than what is interpretation of spectrum correlation function (-fs/2 to fs/2) of that particular alpha. Alpha’s are sufficient condition to know whether hidden periodicity are there or not . Then is it require to examine that particular cyclic frequency spectral density ?

please clarify the about doubt

Reply
1. Chad Spooner says:
  
  December 23, 2019 at 10:00 am
  
  I’m afraid I don’t understand your question here.
  
  Then is it require to examine that particular cyclic frequency spectral density ?
  
  Required for what purpose?
  
  Reply
  1. Hari prasad says:
    
    December 23, 2019 at 8:20 pm
    
    Sorry for not conveying my question properly. Any way i got my answer from above replies
    
    Reply