A noise-free version of the 2018 CSP Blog dataset CSPB.ML.2018R2 is posted here. This allows researchers to correctly apply propagation-channel effects to the generated signals, and to easily add their own noise at whatever level they wish.
The format of the files is the same as CSPB.ML.2018R2, and the truth parameters for each file are the same as the truth parameters for the corresponding file in CSPB.ML.2018R2, except for SNR, which is infinite.
Dear Dr.Chad,
Your maintenance of the CSPB.ML dataset is a valuable resource for the CSP research community.
I am a beginner in CSP and my current paper is using your CSPB.ML.2018 and CSPB.ML.2022 datasets for machine learning classification tasks. Since the model trained directly on the I/Q components is not general enough, I adopted FAM to extract cyclic spectrum features as input to the neural network.
Due to hardware and framework limitations, I have to reduce the original 32,768 sample signal to only 1,024 samples. When using FAM, does selecting a 1,024 sample segment directly from the I/Q components give enough information for classification? Or is it necessary to use downsampling methods such as multi-stage anti-aliasing filtering or FFT-based truncation?
Welcome to the CSP Blog Ruilin! Thanks for the comment.
Maybe. The quality of the spectral-correlation, cyclic-autocorrelation, or cyclic-cumulant estimates depends on several things, including the number of samples, but also the SNR, and the lengths of the underlying statistical periods. For example, if you have 1024 samples of a BPSK signal, and the symbol rate of that BPSK signal is 1/100, then that 1024 samples represents only 10 symbols. Generally you would like to process in the hundreds of periods of the periodicities related to the cycle frequencies. That is, since a key cycle frequency is the bit rate, or symbol rate, you want to process at least low hundreds of symbols.
Additionally, the variance of CSP estimates is a function of the number of samples processed and the effective spectral resolution, as explained in the post on the resolution product.
Here is a measurement result for the spectral correlation function:
Downsampling the 32,768-sample signal won’t matter unless you distort the signal in the process. See the resolution-product post: what matters is the product of the processing time (measured in seconds) and the effective frequency-resolution product (measured in Hz).
Hello Chad,
The new dataset still includes the carrier frequency offset (CFO), correct?
Thanks
Yes, that is the intention. It should be the same as the noisy dataset except for the noise. Let me know if you disagree!
Thank you very much for providing the noise-free version! I’ve been grappling with the technical comparison between 64QAM and 256QAM for years, and I believe one of the primary challenges lies in noise interference and symbol duration issues. This noise-free scenario will be an ideal test case.
You are welcome!
I don’t think the difficulty in distinguishing 64QAM from 256QAM is due to noise or symbol-duration issues. I think it is a more fundamental issue, and that should make it a difficult task for any classifier, whether a trained neural network or a mathematically derived signal-processing algorithm.
The two signals are difficult to distinguish because they share highly similar statistical properties, which follow from their more fundamental probabilistic properties. They share similar probability structure and also probabilistic parameters. These are also similar for all square-constellation digital QAM signals (e.g., QPSK, 16QAM).
By “probability structure” I mean most generally the set of all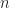
th-order joint probability density functions. Such functions are completely determined by the set of all possible (including conjugation configurations) 
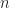th-order moments and also, equivalently, by the set of all possible 
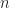th-order cumulants.
By “probabilistic parameters” I mean the specific numerical values for moments and/or cumulants.
The probability structure of a signal leads to the cycle-frequency pattern exhibited by that signal, which we’ve visualized in the cumulant gallery for a large number of signals. All the square-constellation digital QAM signals exhibit the same cycle frequency pattern. The exact values of the cyclic cumulants that make up those patterns vary by the signal type. If we keep the pulse shaping functions for the signals the same, then these probabilistic parameters differ between the signals only by the influence of the moments and cumulants of the symbol random variable.
The issue is that as the “M” in MQAM gets larger, the sets of moments or cumulants become more similar. Let’s take four square-constellation QAM signals as examples: QPSK, 64QAM, 256QAM, 1024QAM. Here are the even-order cumulants of the corresponding symbol random variable starting with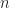
=2, and using 
conjugated factors:
QPSK: 1, -1, 4, -34, 496
64QAM: 1, -0.62, 1.80, -11.5, 127.5
256QAM: 1, -0.60, 1.73, -11.0, 120.1
1024QAM: 1, -0.60, 1.72, -10.8, 118.4
So it should be difficult to distinguish large-alphabet square-constellation digital QAM signals from each other because they are statistically similar.