About

I am a signal processing researcher specializing in cyclostationary signal processing (CSP).

I am hoping to use this blog to help students and researchers learn the basics of CSP, and also to help me learn about new applications of CSP techniques. Since this is a blog, I’ll also post rants, compliments, pet peeves, tips-n-tricks, paper reviews, data sets, etc.

You can leave comments on the posts or contact me at cmspooner @ ieee . org.

Please see this post for information about how best to obtain my assistance with your CSP work.

For beginners, start here.

17 thoughts on “About”

  1. Greetings. I have an interest in using cyclostationary spectral analysis to extract signal features for a task that I am researching. Would it be possible to share you matlab code that computes the cyclostationary spectral correlation? Thank you.

    Reply

  3. Hi Chad,
    This is Andy, Grace’s husband. I’m working at a Bluetooth Low Energy (BLE) chip company. This morning someone here at work was asking a Signal Processing related question and I went online and googled cyclostationary and saw this blog and recognized your face. Anyway, the question was if there was a way to code a BLE signal so that it would be better detected and decoded in a very noisy ISM band environment (with lots of Wifi and BT and all other 2.4GHz transmitters running). Can CSP be exploited in this situation to boost detection and decoding? Or am I asking a dumb question?
    Thanks.

    Reply

    1. Hey Andy! Thanks for stopping by the CSP Blog and leaving a comment.

      Anyway, the question was if there was a way to code a BLE signal so that it would be better detected and decoded in a very noisy ISM band environment (with lots of Wifi and BT and all other 2.4GHz transmitters running). Can CSP be exploited in this situation to boost detection and decoding?

      Generally CSP is used to do signal-presence detection–is the signal present or not, in spite of the simultaneous presence of noise and interference. I get the sense that you are talking about detection in the demodulation sense. Can we use the theory of cyclostationary signals to allow the creation of a signal and its demodulator that, together, are superior to a signal and demodulator that did not use cyclostationarity?

      For the signal-presence detection problem, there are signal-design decisions that can enhance the ability of various CSP detectors to detect the signal. An example is when using pulse-shaping filters in digital QAM/PSK signaling. Keeping the power constant, if you use a larger roll-off in your square-root raised-cosine transmission filter, you will have stronger cyclic features to use in CS-exploiting detectors like the single-cycle detector or the SSCA. You can also spread the signal as in direct-sequence spread-spectrum signaling, and this creates a large number of features with different strengths relative to the signal power, increasing the chance that a CS detector will find some of them. (The different features will be affected differently by interference.)

      For the demodulation/decoding problem, there is the possibility of using frequency-shift (FRESH) filters (I haven’t finished my CSP Blog post on FRESH filters; see The Literature [R6] and My Papers [45,46]), which Grace knows about. There are a lot more papers out there on the topic of communication-signal/system design with FRESH filtering as an integral part of the system.

      You would have to commit to using a demodulation scheme that employed a linear periodically time-varying filter (another name for FRESH filtering) instead of more standard time-invariant components, and you’d have to try to jointly design the signal and the FRESH filter to try to maximize performance in the expected interference environment (which is pretty terrible in the ISM band). But FRESH filters are tricky to adapt. The easiest thing to do is to periodically send a known training sequence, but that is a tough sell when you’re trying to maximize user throughput and want high user bandwidths. FRESH filters can help when the main problem is cochannel interference. For just strong noise, spread spectrum will be helpful, but again, you will have to sacrifice information rate.

      Anyway, that’s my take as a signal processor rather than a real communications engineer.

      Reply

  4. Hi Chad,

    Thank you so much for taking the time to respond to my questions so quickly! It was very helpful. I already forwarded it to the person who asked (the CEO himself). It will take some time for people here to think about it and to see what can be implementable since some of the controller layer is hardware and cannot be changed. Also we are not sure how much filtering constraint we have to be still considered Bluetooth compliant. We’re not very constrained by throughput since most of our customers’ applications will most likely be throughput critical. Your training sequence idea may be more doable. Thank you again for your valuable input.

    Reply

  5. Greetings. I have an interest in understanding the cyclostationary spectral alysis. Now a problem is bothering me：Why many papers mention that the coherence coefficient is equal to 1 when the signal multiplication should be complex. For example: in JOURNAL OF LIGHTWAVE TECHNOLOGY, VOL. 39, NO. 9, MAY 1, 2021. why s_x_alpha(f)=1 since E_T(t,f+alpha/2)*E_T*(t,f-alpha/2) should be a complex signal.
    Sincerely,
    Douglas

    Reply

    1. Hey Douglas! Thanks for stopping by the CSP Blog and leaving a comment.

      I don’t have access to the Journal of Lightwave Technology. If you’d like, you can send me a copy of the paper in question via email.

      The coherence is a complex-valued function that resides on the closed unit disk in the complex plane. As such, it has a maximum magnitude of 1. We typically don’t have much use for the phase of the coherence, and focus on the magnitude. This is a number on the closed interval [0, 1]. When considering many kinds of communication signals without added noise, the coherence magnitude is actually equal to one for one or more cycle frequencies and many values of spectral frequency (see The Literature [R1]). Once noise is added, the values of the coherence magnitude are less than one, except for the non-conjugate coherence for \alpha=0, which is always equal to 1.

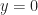      More generally, if I have a complex variable or function, it is perfectly acceptable for that variable or function to take on real values. The real numbers are a subset of the complex numbers. Every real number x is just the complex number x + iy, where y=0. So even the complex-valued coherence can be equal to 1.

      Reply

    2. Douglas:

      I sent you an email asking if you could send me a copy of the Lightwave Technology paper in question (sent on 3/25/22). Did you receive that email? Can you send the paper?

      Reply

  6. Hi Chad,

    I’m new to the blog and cyclostationary processes. Do you have an article that shows to compute the average power for a cyclostationary process? For a WSS process, it’s simply the area under the PSD. What is the equivalent for cyclostationary processes?

    Cheers,
    Mansoor

    Reply

    1. Welcome to the CSP Blog Mansoor! And thanks for the question.

      Are you actually concerned with stochastic processes or are you using the term loosely and are in fact concerned with signals (time-series or the sample paths of a process)?

      If we stick to signals we can generate, receive, record, etc., then the average power of the signal is always equal to the integral of the power spectrum, even when you consider infinite-duration signals.

      If you are working with random processes and their sample paths, and wondering about power and PSDs in one domain versus power and PSDs in the other, then there are some pitfalls if you are using phase randomization. You might want to study The Literature [R68]. For some more basic material on random processes, phase randomization, cyclostationarity, and stationarity, see my posts:

      Stationary vs Cyclostationary

      SPTK: Random Processes

      Let me know if these tips don’t help. Throughout the CSP Blog, I compute a signal’s average power by either simply calculating the variance of the signal’s samples (equivalently, looking at the autocorrelation function at lag \tau = 0) or by integrating the power spectrum. I’m always careful not to do phase randomization unless I’m illustrating why phase randomization ruins cyclostationarity and ergodicity.

      Reply

      1. Hi Chad,

        Thank you for such a prompt response. I’m indeed dealing with signals. I have been religiously reading the articles on the blog including the two you linked. Perhaps I can be more specific with my question.
        When I compute the cross correlation between two discrete-time signals, it is a function of both time “t” and lag “tau”. Moreover, it is periodic in “t”, making it cyclostationary. My goal is to compute the total power of this cross correlation. After computing the PSD (which depends on cyclic freq. alpha), do we just integrate it assuming alpha=0 (as shown in your post linked below), or do we additionally need to sum over all alpha? I guess I’m confused about how total power is defined for cyclostationary signals. I see conflicting definitions in different sources.

        https://cyclostationary.blog/2015/09/28/the-spectral-correlation-function/

        Mansoor

        Reply

        1. When I compute the cross correlation between two discrete-time signals, it is a function of both time “t” and lag “tau”.

          I’m skeptical here. What do you mean, exactly, by “compute” in this sentence? Because the cross correlation for two cyclostationary processes is indeed a function of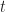 t and lag \tau, but is not computable from data (without invoking cycloergodicity and using infinite time), and the cross correlation between two cyclostationary signals is also a function of t and \tau, but to get at that you have to find all the cyclic autocorrelation functions and add them up in the defining Fourier series.

          As opposed to: I’ve got two signals, and I want to know what their cross correlation is, so I just use something like xcorr.m in MATLAB.

          My goal is to compute the total power of this cross correlation.

          I don’t use the phrase “power of this cross correlation.” So you’ll have to define that. Do you mean something like

          \displaystyle \lim_{T\rightarrow\infty} \frac{1}{T} \sum_{t=-T/2}^{T/2} \sum_\tau |R_{xy}(t, \tau)|^2 ?

          Is that what you want/need?

          When you asked about power, I thought you meant the power of the signal or process, which is the typical use of ‘power.’

          I guess I’m confused about how total power is defined for cyclostationary signals. I see conflicting definitions in different sources.

          Now you are talking about the “power of a signal.” You can escape this swirling loop of thoughts, perhaps, if you just resort to the definition of the power of a signal, which is just the average of the magnitude-squared value of the signal over all time. You could apply that basic definition to either the signals themselves (x(t), y(t)) or to the time-varying cross correlation, since it is just another signal.

          Do you have an expression for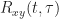 R_{xy}(t, \tau) or an estimate on a computer?

          Can you point me to the sources of the conflicting definitions?

          Reply

          1. Instead of “compute”, I should have said “evaluate the expression”. Yes, I have the expression for R_xy(t,tau) which in my problem is needed to evaluate the autocorrelation of a an error signal R_e(t,tau). This error process is cyclostationary, and I have found its “cyclic autocorrelation function” R_e(tau,alpha) through Fourier Series expansion as shown in one of your blogs. Furthermore, I have also found its “spectral correlation function” S_e(f,alpha) by taking the Fourier Transform of R_e(tau,alpha). My question is how to compute the total power of the error process using S_e(f,alpha)? I understand we need to integrate it over all “f”, but how about “alpha”? In your blog post I linked, you simply let alpha = 0. I thought this was only valid for a WSS signal with a “conventional autocorrelation function”. I would think that for a cyclostationary signal, we need to sum over all “alpha” after integrating over “f”.

            As for conflicting definitions, I was referencing “Probability and Random Processes for Electrical and Computer Engineers” by John Gubner. He briefly discusses cyclostationary processes at the end of Chapter 10, but doesn’t bother defining “cyclic frequencies” at all. To evaluate the expression for the PSD of a cyclostationary signal, he time averages its autocorrelation R_x(t,tau) over one period and then takes the Fourier Transform. I’m not sure if this is rigorously correct.

          2. My question is how to compute the total power of the error process using S_e(f,alpha)? I understand we need to integrate it over all “f”, but how about “alpha”?

            OK, I see, I think. The power of the sample path e(t) is defined by

            \displaystyle P_e = \lim_{T\rightarrow\infty} \frac{1}{T} \int_{-T/2}^{T/2} |e(t)|^2 \, dt

            or by the discrete-time counterpart to that definition.

            I note that the autocorrelation for sample path e(t) is

            \displaystyle R_e^0(\tau) = \lim_{T\rightarrow\infty} \frac{1}{T} \int_{-T/2}^{T/2} e(t+\tau/2) e^*(t-\tau/2) \, dt

            so that

            R_e^0(0) = P_e.

            Now let’s suppose you obtained your expression for {\cal{R}}_e(t, \tau) using the conventional stochastic-process framework for the process e(t). Then you have (as you say above)

            \displaystyle {\cal{R}}_e (t, \tau) = \sum_{\alpha} {\cal{R}}_e^\alpha (\tau) e^{i 2 \pi \alpha t}

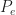            Now, if the process e(t) is cycloergodic, then R_e(t, \tau) = {\cal{R}}_e(t, \tau), and so we can obtain P_e from the stochastic autocorrelation,

            P_e = R_e^0(0) = {\cal{R}}_e^0 (0) = \int {\cal{S}}_e^0 (f) \, df

            If e(t) is not cycloergodic (because you introduced one or more phase-randomizing random variables in your mathematical modeling), then it is not certain that you can integrate the stochastic-process power spectrum to get the power for the sample path.

            You could then check this result by generating multiple long sample paths e_i(t) and directly measuring their power. With probability one, those power measurements should be the same (asymptotically) as the value computed from the random-process development.

            So I think, based on my very limited insight into your mathematical development, that you might want to look into The Literature [R68].

            Buying it?

          3. Another way to think about this is to consider what would happen if you did integrate all the features in an attempt to get at the power.

            Consider two BPSK signals. One has a rectangular pulse function, the other a square-root raised-cosine pulse with rolloff of 0.35. They each have unit variance and symbol rates of 0.1. That is, the measured power of each signal is one, or zero decibels. They have the same observable power.

            We can estimate each of the known non-conjugate spectral correlation functions for each signal and integrate their magnitudes. We expect that the integrated magnitude of the non-conjugate feature for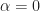 \alpha =0 will be one, since these are sample paths from cycloergodic random processes, and we know that the stochastic PSD will integrate to one because we know that the variance (non-conjugate autocorrelation evaluated at lag of zero) is one.

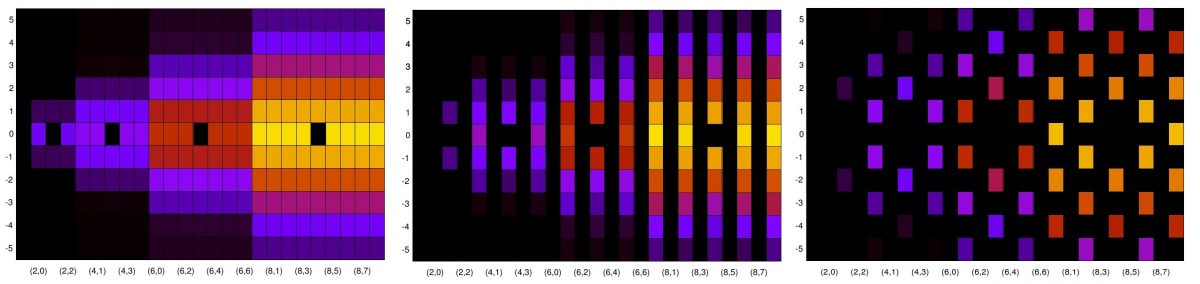
            So, same signal power in each case. What is the sum of the integrated absolute values of the spectral correlation function in each case. I computed them:

            The sum of the integrated features for the SRRC signal is 1.17 and for the rectangular-pulse signal it is 3.75. You can see that the PSDs both integrate to one, as expected.

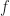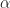            So integrating over both f and \alpha cannot be a correct path to finding the power of a signal.

            For Gubner, if the signal is not almost cyclostationary (there is a single period of cyclostationarity), then for each fixed autocorrelation lag \tau, the described averaging will leave only 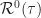{\cal{R}}^0(\tau). So if the involved process is cycloergodic, then his method of finding the power is consistent with what I’ve been saying.

Leave a Comment, Ask a Question, or Point out an Error

%d