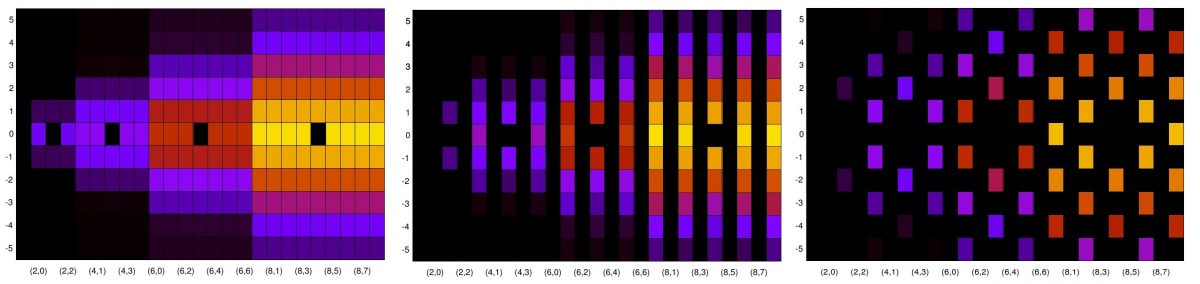
ODU doctoral student John Snoap and I have a new paper on the convergence of cyclostationary signal processing, machine learning using trained neural networks, and RF modulation classification: My Papers [55] (arxiv.org link here).
Previously in My Papers [50-52, 54] we have shown that the (multitudinous!) neural networks in the literature that use I/Q data as input and perform modulation recognition (output a modulation-class label) are highly brittle. That is, they minimize the classification error, they converge, but they don’t generalize. A trained neural network generalizes well if it can maintain high classification performance even if some of the probability density functions for the data’s random variables differ from the training inputs (in the lab) relative to the application inputs (in the field). The problem is also called the dataset-shift problem or the domain-adaptation problem. Generalization is my preferred term because it is simpler and has a strong connection to the human equivalent: we can quite easily generalize our observations and conclusions from one dataset to another without massive retraining of our neural noggins. We can find the cat in the image even if it is upside-down and colored like a giraffe.
Continue reading “The Next Logical Step in CSP+ML for Modulation Recognition: Snoap’s MILCOM ’23 Paper [Preview]”