Comments on “Cyclostationary Correntropy: Definition and Application” by Fontes et al

Update: See also some other reviews/take-downs of cyclic correntropy on the CSP Blog here and here.

I recently came across a published paper with the title Cyclostationary Correntropy: Definition and Application, by Aluisio Fontes et al. It is published in a journal called Expert Systems with Applications (Elsevier). Actually, it wasn’t the first time I’d seen this work by these authors. I had reviewed a similar paper in 2015 for a different journal.

I was surprised to see the paper published because I had a lot of criticisms of the original paper, and the other reviewers agreed since the paper was rejected. So I did my job, as did the other reviewers, and we tried to keep a flawed paper from entering the literature, where it would stay forever causing problems for readers.

The editor(s) of the journal Expert Systems with Applications did not ask me to review the paper, so I couldn’t give them the benefit of the work I already put into the manuscript, and apparently the editor(s) did not themselves see sufficient flaws in the paper to merit rejection.

It stings, of course, when you submit a paper that you think is good, and it is rejected. But it also stings when a paper you’ve carefully reviewed, and rejected, is published anyway.

Fortunately I have the CSP Blog, so I’m going on another rant. After all, I already did this the conventional rant-free way.

The paper is about a particular nonlinear transformation of a signal, and how to represent and exploit a representation of that transformation. Sounds familiar, right?

Let’s ignore Section 2.1, which reviews cyclostationarity, and begin with Section 2.2, which reviews the correntropy function. Equations (9)–(11) are reproduced here:

\displaystyle V_x(t, \tau) = E[G_\sigma (x(t), x(t+\tau))] \hfill (9)

\displaystyle G_\sigma (t, t+\tau) = \frac{1}{\sqrt{2\pi}\sigma} e^{- \frac{(x(t) - x(t+\tau))^2}{2\sigma^2}} \hfill (10)

\displaystyle V_x(t, \tau) = \frac{1}{\sqrt{2\pi}\sigma} \sum_{n=0}^\infty \frac{(-1)^n}{2^n \sigma^{2n} n!} E[(x(t) - x(t+\tau))^{2n} \hfill (11)

I see no problems here. Equation (11) follows from the definition of correntropy and the series expansion of e^x. The critical question is about the expectations in the sum over n. The authors suggest that these expectations could be periodic or polyperiodic functions of time when x(t) is cyclostationary, and so one may extract the Fourier coefficients from such periodic functions by the usual formula, which appears in (18),

\displaystyle V_x^\alpha (\tau) = \left \langle G_\sigma(x(t), x(t+\tau)) e^{-i 2\pi \alpha t} \right \rangle \hfill (18)

where \left \langle \cdot \right \rangle denotes our familiar infinite-time averaging operation.

So far, so good. Then the authors want to represent G(\cdot) as a Taylor series, as before, and this is where things go wrong. We should see the following

\displaystyle V_x^\alpha (\tau) = \left\langle \frac{1}{\sqrt{2\pi}\sigma} \sum_{n=0}^\infty \frac{(-1)^n}{2^n\sigma^{2n} n!} (x(t) - x(t+\tau))^{2n} e^{-i2\pi \alpha t} \right\rangle \hfill (A)

which is a sum of a bunch of different cyclic temporal moment functions.

But the authors combine the complex exponential e^{-i2\pi \alpha t} with the G(\cdot) function and then attempt to expand that single exponential function. They write Equation (20)

\displaystyle V_x^\alpha(\tau) = \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} \frac{1}{\sqrt{2\pi}\sigma} \sum_{n=0}^\infty \frac{(-1)^n}{2^n \sigma^{2n}n!} E\left[ (x(t) - x(t+\tau))^2 + 2\sigma^2 - 2 i \sigma^2 2 \pi \alpha t\right]^n \, dt \hfill (20)

(where they went back to the formulation of the cyclic component as the Fourier-series coefficient of the time-varying expected value). Here I see a sign error on the last term in the bracket, and an extra/mysterious term 2\sigma^2 inside the bracket.

They then invoke cycloergodicity (see also my post on random processes and one on stationarity vs cyclostationarity) and return to the infinite-time averaging operation on the signal x(t) itself to claim (21):

\displaystyle V_x^\alpha (\tau) = \frac{1}{\sqrt{2\pi}\sigma} \left\langle \sum_{n=0}^\infty \frac{(-1)^n}{2^n \sigma^{2n} n!} \left[ (x(t) - x(t+\tau))^2 + 2\sigma^2 - 2i\sigma^2 2 \pi \alpha t]^n \right] \right\rangle \hfill (21)

So now the infinite-time averaging operation includes time averages of powers of t.

In (22) through (25), the authors attempt to deal with this infinite sum. They lump all the bad terms involving powers of t and products of t and the signal x(t) into a function called \xi_\sigma^\alpha(t, \tau), which is not explicitly written out. They get to (24),

\displaystyle V_x^\alpha(\tau) = \frac{\left\langle e^{-i2\pi\alpha t} \right\rangle}{\sqrt{2\pi}\sigma} + \frac{1}{2\sqrt{2\pi}\sigma^3} \left\langle [x^2(t)  + x^2(t+\tau) - 2 x(t)x(t+\tau)] e^{-i2\pi\alpha t} \right\rangle  + \frac{1}{\sqrt{2\pi}\sigma} \left\langle \xi_\sigma^\alpha (t,\tau) \right\rangle \hfill (24)

Then they say

“… assuming x(t+\tau) = x(t) as it tends to infinite [sic] in (24)”

(which is not true), and get (25)

\displaystyle V_x^\alpha(\tau) = \frac{1}{\sqrt{2\pi}\sigma} \left( \left\langle e^{-i2\pi\alpha t} \right\rangle - \frac{R_x^\alpha (\tau)}{\sigma^2} + \frac{\left\langle x^2(t) e^{-i2\pi \alpha t} \right\rangle}{\sigma^2} + \left\langle \xi_\sigma^\alpha(t, \tau)\right\rangle \right) \hfill (25)

which is wrong. Here we know that the x^2(t) term in (24) leads to R_x^\alpha(0), the x^2(t+\tau) term is a phase-shifted version of that term, namely e^{i2\pi\alpha\tau}R_x^\alpha(0), and the cross term gives rise to -2 R_x^\alpha(\tau).

Moreover, the first term in (25) is simply the infinite-time average of a complex sine wave, which is unity for \alpha = 0 and zero for all other \alpha. Yet the authors state

“Besides, Eq. (25) shows that a sinusoisal [sic] function is always responsible for phase shifting the response regardless the [sic] stochastic process type. This property is due to the term \left\langle e^{-i2\pi\alpha t} \right\rangle.”

But that term is either 1 (\alpha = 0) or 0 (all other \alpha), so can’t shift the phase of anything.

So I claim the theoretical development here is fundamentally flawed and nonsensical. The problem is that a lot of the mathematical development is hidden in the mysterious \xi_\sigma^\alpha (t, \tau) function. In my work on higher-order cyclostationarity, I take the opposite approach: What can we say about the utility of just the unique statistical information associated with each order n? I try to separate all the contributions to the signal’s probability density functions due to different moment/cumulant orders. These authors’ mission is to intentionally mix them all together. Why not just expand (A) above, and identify the various terms using previously defined functions? The various cyclic moments just fall right out of that expression.

The simulations section is also seriously flawed. First, why not compare their correntropy structure with something optimal or close, such as the single-cycle or multicycle detectors? Second, the frequency axes on the figures are quite hard to understand in light of the values in Table 1. The axes are labeled with normalized frequency (\alpha/f_s), the table tells us the carrier is 80 MHz and the sampling rate is 320 MHz, so the doubled-carrier feature for their BPSK signal should be at 160 / 320 = 0.5. Instead it is shown at 8e-7 (Fig 2). And the symbol rate shows up at 1e-7 but should be 2/320 = 0.00625.

I also don’t believe Steps 3 and 4 of the algorithm in Section 4.1 can work in general. This is like the time-smoothing method, but they’ve left off the complex phase factor that accounts for the relative delay between the successive blocks. It will work provided the cycle frequencies that are exhibited by the signal in the data are equal to k/N, where N is the block length, but otherwise it won’t. In the real world, the cycle frequencies are almost never that convenient.

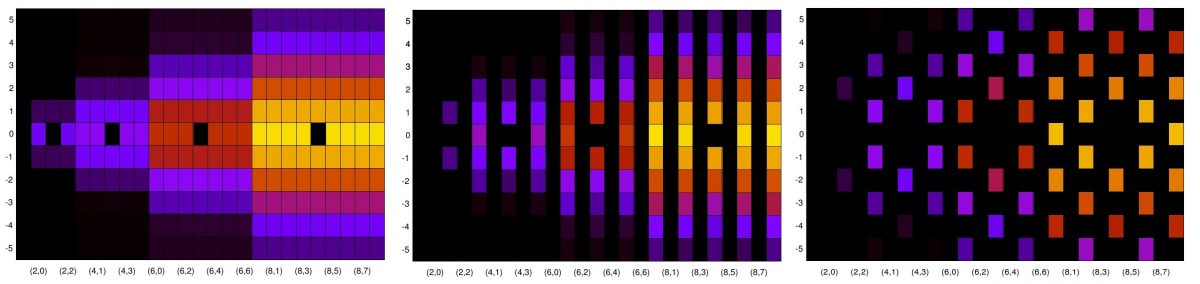
In Figure 6, where is the evidence that higher-order information is coming into view? The appearance of the small harmonics of 1e-7 is not explained. For BPSK, we’d expect to see evidence of the quadrupled carrier (which is quite strong), as well as the doubled carrier, but we see in the four plots mostly just the typical second-order cycle-frequency pattern for textbook BPSK.

Finally, the probabilities of detection for the author’s correntropy method are achieved at SNRs of more than 12 dB less than those for the competing cyclostationary method. The author’s show that the conventional spectral correlation function for the noisy BPSK signal is completely obliterated (Figure 3). So we are to believe that the noise absolutely destroys the second-order cyclostationarity, but magnificently preserves the higher-order cyclostationarity, so that excellent detection results are obtained. Hmmm….

I have more objections, but I’ve run out of energy for this. Let me know if you disagree with me about this paper, or if I’ve went wrong somewhere in analyzing it.

Author: Chad Spooner

I'm a signal processing researcher specializing in cyclostationary signal processing (CSP) for communication signals. I hope to use this blog to help others with their cyclo-projects and to learn more about how CSP is being used and extended worldwide.

5 thoughts on “Comments on “Cyclostationary Correntropy: Definition and Application” by Fontes et al”

  1. Hello Dr. Spooner. We would like to first thank you for your time in reviewing the paper and point out its weakness. Let us assure you that we are trying to prepare an “erratum” and will send to the Journal. Please allow us to answer each of your comments separately bellow. We also would like to express our regret with the intensity with you frame our mistakes (this might be prejudicial to us). As we going to argue, our intentions were the best in making a good contribution and we think we did.

    About the Taylor series analysis, it is one of many aspects of the paper. As we are going to explain, you are right in the technical arguments but wrong in its interpretation. Out goal is only to show a property of correntropy that it CONTAINS the information of conventional second order cyclostationarity (thats it!). As we mention in the paper:

    “Eq. (20) is merely interpretative, as it is not recommended for the calculation of the CCF.”

    With that, we hoped anyone could understand that the derivation had only an interpretative purpose. Also, its contribution (of the second order term $R_{alpha}(tau)$) is emphasized when the kernel size is large. You can see that in the results. Figure 6(d) shows the alpha profile of a BPSK that look very much like the second order cyclostationarity. That is an interesting result because our method, in a sense, extends the conventional method and can be tuned by a single parameter.

    We do not intent to compete with any method more than science allow as being productive. Please do not feel threatened by correntropy. Eventually, your method is better than ours. But the intention was to present a new approach that has a kernel based ground. We tried to incorporate all of your comments in the fist time you rejected out paper and submitted to a journal with a faster response time. Our group is composed almost entirely with small researchers that are trying to incorporate correntropy into algorithms that used correlation as a measure of some kind. We think that is a good and valid research topic even if eventually it does not perform as good as the best state of the art methods.

    We always try to work in a serious manner but errors could happen. We hope you realize that, as serious as we tried to be, we cited your work as a state of the art in the paper. Actually, we are now working on an extension of this paper and we would like to propose your namer as a reviewer, if you agree. We have a bit of experience with correntropy. Although we worked and applied conventional cyclostationarity in some problems, we thrust you with fat more experience than ourselves. We think this new paper would benefit strongly if we could count on you as a reviewer. Nevertheless, we would like to ask you to be open to new research philosophies and approaches. If you please answer this replica in your blog, be kind. Please do not imprison yourself with textual details. Do not consider this reply as a technical and solid argument. Instead, consider as a informal letter with a simple explanation of our intentions when published the research.

    “(where they went back to the formulation of the cyclic component as the Fourier coefficient of the time-varying expected value). Here I see a sign error on the last term in the bracket, and an extra/mysterious term 2\sigma^2 inside the bracket.”

    In fact you are right about the sign the extra term. Equations 21a to 24 have no extra term. And we really made a typo in putting the sigma^2 and the minus sign of the beta.

    “In (22) through (25), the authors attempt to deal with this infinite sum. They lump all the bad terms involving powers of t and products of t and the signal x(t) into a function called \xi_\sigma^\alpha(t, \tau), which is not explicitly written out. They get to (24)”

    The intention is exactly overlook the hi-order terms, although we still explicitly write them in the expression. Remember that we do that and explicitly show that for large sigmas this term becomes negligible. As we said, you misinterpreted the purpose of the derivation. The Taylor expansion do NOT aim to produce a new hi-order cyclostationarity method by itself.

    “Then they say “… assuming x(t+\tau) = x(t) as it tends to infinite [sic] in (24)” (which is not true), and get (25)
    which is wrong. Here we know that the x^2(t) term in (24) leads to R_x^\alpha(0), the x^2(t+\tau) term is a phase-shifted version of that term, namely e^{i2\pi\alpha\tau}R_x^\alpha(0), and the cross term gives rise to -2 R_x^\alpha(\tau).”
    that is exactly what we wanted to show (appearance of $R_{alpha}(\tau)$)”

    You are right again. We confused E{x(t)}=E{x(t+tau)} for stationary process instead of CYCLEstationary ones (the infinity term used in the sentence was a misplace about the experted value). We tried to compact the notation and under thought the math… In fact this is such an obvious mistake that we really feel embarrassed by it (saying this publicly and humbling apologizing in your blog)

    “Moreover, the first term in (25) is simply the infinite-time average of a complex sine wave, which is unity for \alpha = 0 and zero for all other \alpha. Yet the authors state”

    agreed

    “But that term is either 1 (\alpha = 0) or 0 (all other \alpha), so can’t shift the phase of anything.””

    Here we really confused textually the shifting present in the term $x^2*e^{…}$ with the first term that only adds a “delta” to the result. Again we feel embarrassed and apologize publicly here.

    “So I claim the theoretical development here is fundamentally flawed and nonsensical. The problem is that a lot of the mathematical development…”

    Since the goal of the development is to show only the appearance of $R_{alpha}(\tau)$, there is no problem in lumping the terms. So there is no flaw in that. If you didn’t have understood our objective, you would not call it nonsensical. Here, either you failed to understand or we failed to explain. Either way, you were unfair in accusing us of writing nonsense. If you had contacted us and we still kept the “nonsense”, than you would have the right to call that.

    “The simulations section is also seriously flawed. First, why not compare their correntropy structure with something optimal or close…”

    Explained in the introduction of this reply.

    “I also don’t believe Steps 3 and 4 of the algorithm in Section 4.1 can work in general. This is like the time-smoothing method, but they’ve left…”

    Step 3 in the algorithm is needed because correntropy always leaves a DC value considerably larger than conventional correlation (it has no negative values). Those steps only rids the final plot of the central peak at the center of the final alpha profile. This step improves the final feature descriptors and its merely of practical use.

    “In Figure 6, where is the evidence that higher-order information is coming into view? The appearance of the small harmonics of 1e-7 is not explained…”

    The goal of correntropy is NOT to REPRODUCE the hi-order statistics of random signals. We do not expect to see ANY specific moment when applying correntopy. Instead it works as a non-linear transformation that COMBINES moments in such a way that give us some descriptors that otherwise were not possible with a simple correlation.

    “Finally, the probabilities of detection for the author’s correntropy method are achieved at SNRs of more than 12 dB less than those for the competing…”

    Same as explained in introduction…

    Finally, you mentioned that there is more mistakes you can point out. Since we are going to prepare an erratum, we would appreciate very much if you actually point out those mistakes so we can improve the erratum.

    Thanks

    Best, Aluisio Fonte, Allan Martins, Joilson Rego and Luiz F. Silveira(authors)

    Reply

    1. Perhaps “nonsensical” was an unkind word choice. For that I apologize. I meant something along the lines of “incomprehensible” or “impenetrable.”

      You don’t need my permission to request me as a reviewer (or to request that I not be asked to review), but if I am requested to review a new paper of yours, I will do it.

      The goal of correntropy is NOT to REPRODUCE the hi-order statistics of random signals. We do not expect to see ANY specific moment when applying correntopy. Instead it works as a non-linear transformation that COMBINES moments in such a way that give us some descriptors that otherwise were not possible with a simple correlation.

      Considering this quote, and that you brought up Figure 6 in your comment, I wonder if you can explain Figure 6. You say in the paper that:

      Signal peaks shown in Fig. 6 .(d) for sigma= 1 , extract just second-order cyclostationary information approaching of the Fig. 5 , while the other kernel size provides the extraction of the statistical information of both second- and higher-order for the analyzed signal.

      What in Figure 6 (a)-(c) evidences the higher-order statistical information? Keep in mind that the readers here at the CSP blog already know all the cycle frequencies for BPSK (A(n,m) = (n-2m)fc + k/T).

      Reply

  2. Hello Dr. Spooner, thank you for the clarification.

    About the permission, we were not trying to formally ask your permission to review the paper. We were just kindly inquiring you if you would not be bothered in reviewing it in light of the “strongness” with you negatively commented our work. We have your as an authority in the field.

    About figure 6, let us try to answer your question a bit more systematically.

    1 – Please notice that we are not proposing a method that selectively evidences this or that moment or harmonic in a cyclostationary signal’s alpha profile. When we say “extracts” hi-order moments we mean *combinations* of them (for the gaussian kernel, a combination of the even moments) that provide us with means of obtaining “cyclo-features”.

    1.1 – For instance, the auto-correntropy spectrum of a sine wave has a bunch of harmonics. It *do not* intent to extract the “correct” harmonic or statical “moment”.

    2 – Figure 6 shows a simple example where for the BPSK, a small kernel size produces a CYCLOcorrentropy-alpha-profile (please notice the nomenclature) that is *different* from the second-order-cyclostationary-alpha-profile. They *supposed to be different*! That is the whole point! We want to extract cyclic characteristics (as we say in the paper) that be robust enough to not degenerate in the presence of impulsive noise.
    We fail to see how can you miss that contribution and focus on secondary points (as the taylor expansion), despite the good performance on the results.

    3 – The question about the usefulness of a (apparently) arbitrary cyclic characteristics is a fair question (we imagine that, that would be your next point).

    3.1 – For people that do not understand correntropy, it goes like this: It is a non-linear version of the correlation. Since its invention, people keep re-writing all the algorithms that uses correlation by correntropy versions of it. One that was not yet “taken” was cyclostationarity. It uses the autocorrelation function in its core. Hence we plugged autocorrentropy and got good results.
    We do not see any flaw in this idea…

    Since you did not comment on our replies about the taylor expansion, can we assume the issue were clarified? Can we agree that it has no flaw? As we said, it served only to show the presence of $R_{alpha}(\tau)$ is that flaw?

    As many people read this blog, we would like to be sure that, as professionals, we do not produce “flawed” derivations or results. Thats why we assume our part on the mistakes here (publicly) and will send an erratum to the journal.

    Reply

  3. We would like to try to elaborate a bit more about the results on figure 6.

    We will do that by getting back to reference (Santana, Principe, Santana, & Kardec Barros, 2012) in the paper. That reference explains how auto-correntropy-spectrum works. We will try to summarize the explanation.

    – First we have to remember that correntropy is a “replacement” for correlation. Hence we can define the auto-correntropy-spectrum the same way we define auto-correlation-spectrum (Fourier transform of the auto-correlation/correntropy function).

    As an example, lets consider a pure sine wave signal of some frequency. The auto-correlation-spectrum consists of only one peak representing the frequency of the signal. However, the auto-correntropy-spectrum for small kernel sizes, ads several harmonics of the fundamental signal frequency. Lets explain why that happens:

    — When we perform the computation of the exponential ($exp(-x^2/(2\,\sigma^2))$) for values smaller then 1 in the argument, the signal will rapidly decrease and become near zero. On the other hand, the values close to zero in the signal will have values close to one. In the limit a sine wave will become a Dirac Comb. Thus, is spectrum will also be a Dirac Comb (with frequency spacing equal to the fundamental of the signal). That explains the appearance of “more” peaks in the spectrum.

    For some modulation, what happens is that the creation of the new spectral lines will now have “copies of the signature” of the modulation in each harmonic (harmonic of the fundamental or carrier). Now interesting things happens. If we analyze the limiting case (\sigma \to 0), we will have practically a pulse train as result (similar as you see in figure 6(a)). However, when using intermediate values of kernel sizes some of the harmonics of the modulation COMBINE themselves to make a NEW spectral signature. That combination is not trivial to formally compute. It might be possible, for a given modulation, try to figure the mathematical expression for a given frequency but that is not the point of our paper.

    Now, for the alpha profile, one must extrapolate this line of thinking and imagine several “copies of this scenario” for each value of alpha (cyclic frequency) and imagine them projecting in to the final alpha profile.

    The expected result is the creation of new peaks in the alpha profile that are not easy to measure. The only thing we can expect is the creation of new peaks themselves (that might be combined in some fashion). Hence, in figure 6(a) (small kernel size) we see basically the alpha profile of a Dirac Comb. However, for intermediate values of kernel sizes, we see a different profile from the conventional second order alpha profiles.

    The main contribution is that this new alpha profile is robust to impulsive noise. That happens because of the weighting of large values of the signal by the exponential. Signals values with amplitude in the range of the kernel size, will be weighted more than values that are much larger (impulses in the noise).

    Yet another interesting thing is that for large sigmas, we have a slow decaying exponential that “shrinks” the scale but behaves like a linear relation of the argument of the exponential. That leads to results that are close to the second order result (with a very large DC component that is easily extracted).

    Reply

Leave a Comment, Ask a Question, or Point out an Error

Discover more from Cyclostationary Signal Processing

Subscribe now to keep reading and get access to the full archive.

Continue reading