Second-Order Estimator Verification Guide

Use this post to help check the accuracy of your second-order CSP estimators.

Update September 2022: New section on the non-conjugate and conjugate coherence function.

***

In this post I provide some tools for the do-it-yourself CSP practitioner. One of the goals of this blog is to help new CSP researchers and students to write their own estimators and algorithms. This post contains some spectral correlation function and cyclic autocorrelation function estimates and numerically evaluated formulas that can be compared to those produced by anybody’s code.

The signal of interest is, of course, our rectangular-pulse BPSK signal with symbol rate 0.1 (normalized frequency units) and carrier offset 0.05. You can download a MATLAB script for creating such a signal here.

The formula for the SCF for a textbook BPSK signal is published in several places (The Literature [R47], My Papers [6]) and depends mainly on the Fourier transform of the pulse function used by the textbook signal.

We’ll compare the numerically evaluated spectral correlation formula with estimates produced by my version of the frequency-smoothing method (FSM). The FSM estimates and the theoretical functions are contained in a MATLAB mat file here. (I had to change the extension of the mat file from .mat to .doc to allow posting it to WordPress–change it back after downloading. It is a zipped .mat file as of 12/2/22.) In all the results shown here and that you can download, the processed data-block length is 65536 samples and the FSM smoothing width is 0.02 Hz. A rectangular smoothing window is used. For all cycle frequencies except zero (non-conjugate), a zero-padding factor of two is used in the FSM.

For the cyclic autocorrelation, we provide estimates using two methods: inverse Fourier transformation of the spectral correlation estimate and direct averaging of the second-order lag product in the time domain.

Power Spectrum

Let’s look at the PSD first. The graph in Figure 1 shows a plot of the theoretical PSD for the signal plus noise and the corresponding FSM estimate. The signal power is one and the noise power is 1/10. The mainlobe and the two adjacent sidelobes match nearly perfectly; there is a small discrepancy three or four sidelobes away from the mainlobe. Overall, I judge this an excellent match between theory and measurement.

study_psd_new
Figure 1. Estimated and theoretical power spectral density (PSD) functions for a rectangular-pulse BPSK signal in noise. The bit rate is 1/10 and the carrier frequency offset is 0.05. The noise power is 1/10 and the signal power is 1.

Non-Conjugate Spectral Correlation

Next consider the non-conjugate cycle frequencies, which are harmonics of the bit rate 0.1. The first three harmonics are 0.1, 0.2, and 0.3, and the theoretical and FSM-estimated non-conjugate spectral correlation function magnitudes are shown in Figure 2.

study_scf_new
Figure 2. Estimated and theoretical non-conjugate spectral correlation function (SCF) magnitudes for the rectangular-pulse BPSK signal with power spectrum shown in Figure 1. The bit rate is 1/10, so these are the SCFs for the bit rate, twice the bit rate, and triple the bit rate.

Conjugate Spectral Correlation

Figure 3 shows three of the conjugate spectral correlation function magnitudes. The conjugate cycle frequencies are equal to the doubled carrier plus harmonics of the BPSK bit rate, or \alpha = 2f_c + k/T_0 = 0.1 + 0.1k. The three functions shown below correspond to k = -1, 0, 1.

study_conjscf_new
Figure 3. Estimates and theoretical conjugate spectral correlation function magnitudes for the rectangular-pulse BPSK signal with power spectral density shown in Figure 1.

Non-Conjugate Cyclic Autocorrelation

Each of the functions above is inverse Fourier transformed and the resulting cyclic autocorrelation estimates are plotted:

study_caf_new
Figure 4. Estimated and theoretical non-conjugate cyclic autocorrelation functions (CAFs) for the rectangular-pulse BPSK signal with power spectral density shown in Figure 1. The estimates are the inverse Fourier transformed (complex-valued) estimates corresponding to the SCF magnitudes shown in Figure 2.

The cyclic autocorrelation functions are also directly estimated in the time domain by simply implementing the defining average:

nc_caf_time_domain
Figure 5. Estimated and theoretical non-conjugate cyclic autocorrelation functions (CAFs) for the rectangular-pulse BPSK signal with power spectrum shown in Figure 1. Here the estimates are obtained by directly implementing the finite-time version of the time-domain definition of the cyclic autocorrelation function.

Conjugate Cyclic Autocorrelation

The conjugate cyclic autocorrelation functions are estimated by inverse Fourier transforming the FSM spectral correlation estimates and by direct time-domain averaging of the lag product:

study_conjcaf_new
Figure 6. Estimated and theoretical conjugate cyclic autocorrelation functions (CAFs) for the rectangular-pulse BPSK signal with power spectrum shown in Figure 1. Here the CAFs are estimated by inverse Fourier transforming the (complex-valued) conjugate spectral correlation function estimates corresponding to the magnitudes shown in Figure 3.
c_caf_time_domain
Figure 7. Estimated and theoretical conjugate cyclic autocorrelation functions (CAFs) for the rectangular-pulse BPSK signal with power spectrum shown in Figure 1. Here the estimates are obtained by direct implementation of the finite-time version of the temporal definition of the conjugate CAF.

Non-Conjugate and Conjugate Coherence Functions

In this final section I use the FSM to estimate the coherence function for several of the BPSK signal’s cycle frequencies. The theoretical coherence function has a maximum magnitude of one, which is always achieved by the non-conjugate coherence for a cycle frequency of zero. That is, the power spectrum is perfectly coherent no matter what the signal. In practice, when we estimate the coherence using an estimate of the spectral correlation (for the numerator) and an estimate of the power spectrum (for the denominator), the value may exceed unity. A good debugging strategy for the coherence is to first focus on getting your code working for the non-conjugate cycle frequency of zero because you know that should be very close to one for all spectral frequencies.

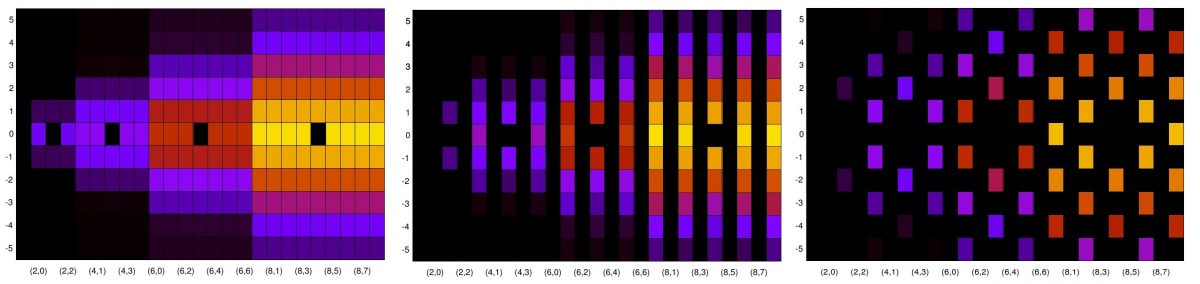
Figure 8 shows the FSM-estimated non-conjugate spectral coherence for a cycle frequency of zero along with the theoretical power spectrum from Figure 1. My implementation of the FSM actually calculates the coherence here–it doesn’t just set it equal to one if it sees the zero cycle frequency.

Figure 8. Theoretical BPSK PSD along with estimated non-conjugate coherence function for a cycle frequency of zero. The theoretical value of this coherence function is unity for all spectral frequencies.

Figure 9 shows the estimated non-conjugate spectral coherence estimates along with the theoretical spectral correlation functions so you can visually line up the peaks.

Figure 9. Measured non-conjugate coherence functions (FSM) along with theoretical spectral correlation functions.

Finally, Figure 10 shows estimated conjugate spectral coherence functions along with their associated theoretical conjugate spectral correlation functions.

Figure 10. Estimated conjugate coherence functions (FSM) along with their theoretical conjugate spectral correlation function counterparts.

Conclusion

The matches between theory and measurement are excellent. This should give you confidence in comparing the results here with the output of your estimator when you use the rectangular-pulse BPSK signal.

Don’t forget to download the MATLAB file containing all the functions plotted in this post (including their time or frequency vectors that define the x-axis) here.

Author: Chad Spooner

I'm a signal processing researcher specializing in cyclostationary signal processing (CSP) for communication signals. I hope to use this blog to help others with their cyclo-projects and to learn more about how CSP is being used and extended worldwide.

18 thoughts on “Second-Order Estimator Verification Guide”

    1. The file is a .mat file, but I renamed it with a .doc filename extension so that WordPress software would allow me to upload it to the blog. Rename the file from theory_and_meas_functions_mat.doc to theory_and_meas_functions.mat and then use ‘load’ in MATLAB. Let me know if that doesn’t work for you, and if it does not, exactly what errors you see.

      Reply

  2. Chad, thank you for this wonderful blog.

    For python users, they can use loadmat() function from scipy.io:
    https://docs.scipy.org/doc/scipy/reference/tutorial/io.html

    However, for certain Matlab versions (including the one used to create theory_and_meas_functions.mat), I was able to open it with hdf5 reader. Here is a sample code to do so:

    import h5py
    f = h5py.File('/my_file_location/theory_and_meas_functions_mat.mat')
    for item in f.keys():
       dataset=f[item]
       print(dataset)
    f.close()

    Reply

  3. Dear Chad,

    Thanks for your information-packed blog !! 🙂
    Implementing things by myself so far has been a real pain, but it is indeed very helpful in understanding the different topics.

    I have implemented a Matlab function for CAF estimation by time-averaging, and the results match what you show in this post (and the content of your archive, e.g., if I compare my NC-CAF estimate for alpha=0.1 to your caf_nc_fsm_1 variable, the two are very very close).
    I have then performed an FFT of each CAF to get the SCF, and there some problems start to arise:

    1) if I display what I assume are your results from the archive, I get extremely weird things. For instance, if I plot the ‘scf_nc_theory_1’ variable with:
    plot(f_theory_nc, 10*log10(abs(fftshift(scf_nc_theory_1))));
    I get the result shown here: https://ibb.co/JFKqJf5
    Is there anything wrong with my command/my assumptions about the archive content?

    2) My result for alpha = 0.1 (https://ibb.co/3zC7PWf) looks very close to what you have in your figure above. However, if I change alpha, for instance for alpha = 0.3, my result is similar in shape but shifted in frequency, see e.g., https://ibb.co/TrXRfLh
    Am I missing something?

    Thanks in advance for your help!
    Best,
    Rob

    Reply

    1. Thanks for reading the CSP Blog Rob! And I appreciate the comments.

      1) if I display what I assume are your results from the archive, I get extremely weird things.

      The theoretical and estimated SCFs in the Verification post mat file are already in dB! You can tell by plotting the PSD, which goes down to the noise floor at -10, and since PSDs can’t be negative in their natural W/Hz units, it must be dB.

      I’ll answer (2) in a separate reply, since you elaborated on it in a separate comment.

      Reply

      1. Here are the plots that one should get when using the various theoretical and measured SCF vectors in the Verification post mat file:

        Just plot the correct frequency vector against the estimate or theory vector without converting to dB.

        Reply

  4. Just thinking some more about point (2): in my CAF code, I use the equation for the asymmetric version, and thus I obtain the symmetric CAF by premultiplying by exp(1i*pi*alpha*tau). This would indeed justify a shift in frequency, but wasn’t this a pre-requisite to get the right result ?

    Reply

    1. Rob:

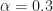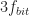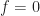      Yes, I see that the non-conjugate SCF for \alpha = 0.3 = 3 f_{bit} is shifted over in frequency. All non-conjugate SCF slices for this test signal should be centered at f= 0.05 (the carrier is 0.05) and all conjugate SCF slices should be centered at f=0. So it looks like your attempt to use the asymmetric CAF estimate has gone slightly wrong. From the Cyclic Autocorrelation post:

      screen shot from cyclic autocorrelation post

      So you have to get the signs associated with \tau right. Perhaps you have a sign error in your phase compensation? Otherwise the shape of the function looks right.

      Reply

      1. (of course) you are right; I did have a (double) mistake, since both the sign in the second x() term of the product and in the phase compensation were wrong; by putting a minus sign in the phase compensation I was able to fix the problem!
        Thanks! 🙂

        Reply

  5. Hi again,

    (I know, I’m on the way to become the most prolific commentator of the blog ;))
    I’ve tried implementing the SCF computation via TSM (your answer on stackoverflow was very helpful for that, my code is close to the one posted there though vectorized — and some values are not 100% the same, for instance both my “ts” and the “i” term in the exponential that you suggest as a shift start from 0).
    I’ve checked the results with those mentioned in my previous comments, as well as (visually) with your figures, and they are virtually identical for the non-conjugated version, but the conjugated versions are completely wrong (and much noisier, though I’m using the noise-free version of the signal, x_of_t).
    Here’s what I get for different alpha values
    https://ibb.co/NtD9sjY
    (signal = your BPSK-rect with T_bit = 10 and f_c = 0.05, N = 64 blocks each with size T = 4096)
    Does this make any sense to you?
    Thanks again! 🙂
    Rob

    Reply

    1. Good news that the non-conjugate estimates are looking good!

      I can’t tell what is going wrong with your conjugate estimates. They are definitely too small in magnitude and highly erratic. In the TSM, you have to pay attention to the values of the shift up and shift down for the various cyclic periodograms that you are averaging, and you have to do the phase compensation of each one as well. I assume that your phase compensation and shift-up/shift-down operations are fine for the non-conjugate case, so it appears that one or both of these is incorrect in the conjugate case. Remember that you need to form the conjugate cyclic periodogram, which is NOT equal to the non-conjugate cyclic periodogram with the conjugation of the second factor left off. The argument of the second factor is different (it is negated, or reversed):

      X_T(t, f+\alpha/2) X_T(t, \alpha/2 -f)

      Reply

      1. I might have *accidentally* neglected that :S 😀
        Just out of curiosity (let’s call it SP101): is there a “nicer” way to get X(-f) other than playing with the conjugates before/after calling the fft() function?

        Reply

          1. Oups, yes, I was thinking super weird stuff when I could just read back the vector from the other end :S
            Thanks for your help! 🙂

  6. Thanks for updating the post with coherence plots. The associated data file (theory_and_meas_functions.mat) doesn’t seem to have been updated with the data for the coherence plots. Any chance you’d be willing to update the data file too?

    Reply

Leave a Comment, Ask a Question, or Point out an Error