The cyclic autocorrelation function (CAF) for rectangular-pulse BPSK can be derived as a relatively simple closed-form expression (see My Papers [6] for example or The Literature [R1]). It can be estimated in a variety of ways, which we will discuss in future posts. The non-conjugate cycle frequencies for the signal are harmonics of the bit rate, , and the conjugate cycle frequencies are the non-conjugate cycle frequencies offset by the doubled carrier, or
.
Recall that our simulated rectangular-pulse BPSK signal has samples per bit, or a bit rate of
, and a carrier offset of
, all in normalized units (meaning the sampling rate is unity). We’ve previously selected a sampling rate of
MHz to provide a little physical realism; let’s do that here too. This choice means the bit rate is
kHz and the carrier offset frequency is
kHz. From these numbers, we see that the non-conjugate cycle frequencies are
kHz, and that the conjugate cycle frequencies are
kHz, or
kHz.
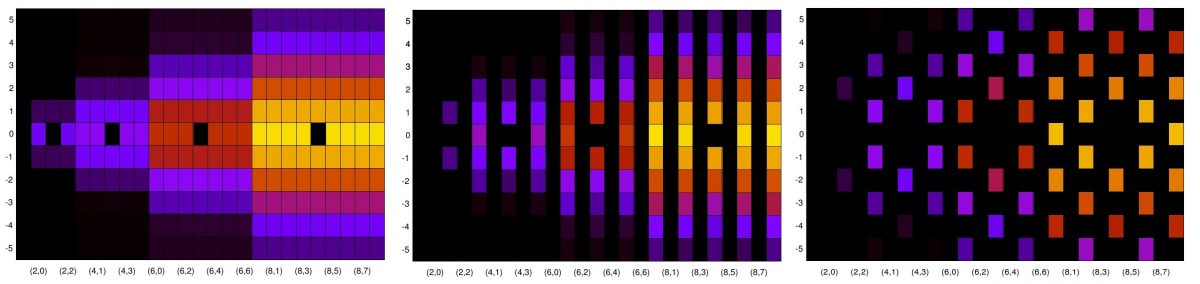
The blindly estimated CAF for our noisy rectangular-pulse BPSK signal is shown here:

The non-conjugate CAF for is the conventional autocorrelation function. Here we can see it is triangular in shape, with an additional inflation of the peak for
, due to the presence of noise, which has non-zero power. For comparison, here is the numerically evaluated theoretical formula for the CAF for rectangular-pulse BPSK:

The match is excellent.
The theoretical formulas for the cyclic autocorrelation and spectral correlation function for BPSK signals (and other digital QAM/PSK signals) can be found in several places. One of the first places it was published is in the book Statistical Spectral Analysis by W. A. Gardner (The Literature [R1], Chapter 12). The formulas for both the th-order reduced-dimension cyclic cumulant and the
th-order cyclic polyspectrum for PAM/PSK/QAM can be found in My Papers [6] and my dissertation. The
-th order cyclic cumulant reduces to a lag-shifted (asymmetric) version of the cyclic autocorrelation for
.
Interpreting the CAF
The non-conjugate CAF can be interpreted as the correlation between the lag product and the complex-valued sine wave
. From that point of view, the CAF
is the complex amplitude of the additive sine wave that is present in the lag product. That is, that sine wave has amplitude
and phase
. Note that the amplitude and phase depend on the delay
. When the CAF is zero, there is no finite-strength additive sine-wave component in the lag product for the value of
chosen; otherwise there is.
The conjugate CAF can be interpreted as the correlation between the lag product and the complex-valued sine wave
.
Some signals may have only non-zero non-conjugate CAF values (such as large-alphabet digital QAM), some only non-zero conjugate CAF values (such as analog amplitude modulation, discounting the ever-present non-conjugate cycle frequency of zero), and some have both (such as our favorite signal, the rectangular-pulse BPSK signal).
Comparison with a Bandwidth-Efficient BPSK Signal
The rectangular-pulse signal has infinite bandwidth, and therefore it possesses an infinite number of cycle frequencies. However, the strength of the cyclic autocorrelation for most of those cycle frequencies is very small, so that in practical terms, the rectangular-pulse signal possesses ten or so significant features. That’s actually quite a lot compared to practical real-world signals like BPSK with square-root raised-cosine (SRRC) pulses. Here is the estimated CAF for a BPSK with SRRC pulses and a pulse roll-off factor of 0.3 (the excess bandwidth is 30%):

The non-conjugate CAF possesses exactly three cycle frequencies, (only two of those are shown in the plot), and the conjugate CAF also possesses three cycle frequencies
. Note also that the width of the CAF is much larger than for the rectangular-pulse signal (the
axes are different between the plots for the two signals). This is a direct consequence of the fact that the rectangular-pulse signal is strictly time-limited whereas the SRRC-pulse signal is strictly bandlimited.
hello, could you please explain why cyclic frequencies in your example are equal to k* (0.1) MHz?
I’ve updated the post to answer your question. Leave a comment if unclear!
please I need an example code for cyclostastionary features detection for bpsk modulation
Hi Ben. The CSP Blog is a self-help blog. I don’t give out much code. Let me know if you get stuck, though, trying to write your own. That’s the only way you’ll really understand CSP.
this is my own code but i don’t know if it’s good to calculate the cyclic autoucorrelation function or not;
please help me where is the probléme in this code
thanks dear in advance.
function [caf2, taus, alphas] = caf2(s)
N1=length(s);
N=floor(N1/3);
caf2 = zeros(2*N+1,N);
prods = zeros(2*N+1,N);
taus=-N:N;
alphas=-pi+2*pi/(N):2*pi/(N):pi;
alphas=alphas/pi;
for tau = taus
for alpha=alphas
stat = (s(N+1:2*N)).*exp(-j*pi*alpha*t(N+1:2*N));
shifted = conj(s(N+1-tau:2*N-tau)).*exp(j*pi*alpha*t(N+1-tau:2*N-tau));
prod=stat.*shifted.*exp(-2*j*pi*alpha*t(N+1:2*N));
prods(tau+N+1,:)=prod;
end
caf2(tau+N+1,:)=fftshift(fft(prod));
end
end
Your code does not run to completion:
>> caf2(s)
Undefined function or variable ‘t’.
Error in caf2 (line 11)
stat = (s(N+1:2*N)).*exp(-j*pi*alpha*t(N+1:2*N));
So you need to fix that first.
I see that you are trying to compute a statistic for a large number of cycle frequencies and delays. I would like to suggest the following: Divide and conquer. Do the simplest things first, then build up to the most complicated. For example, try to estimate the cyclic autocorrelation for just a single cycle frequency (say, zero), and a few delays (tau) near zero. Then try to extend to all delays. Then extend so that you can specify any cycle frequency. Finally, when that is all correct, put it in a loop and call it for as many cycle frequencies as you want.
hey
i would like to know about the theorical formula for bpsk cyclic autocorrelation ?
is there any listed reference?
I’ve updated the post with references that should help you find the answer to your question. Let me know if you still have problems or questions.
thanks ser
please comment :
in witch frequency we have peak
Fs = 5000;
t = 0:1/Fs:1-1/Fs;
s = (cos(2*pi*600*t)+randn(size(t)));
N1=length(s);
N=floor(N1/3);
caf2 = zeros(2*N+1,N);
prods = zeros(2*N+1,N);
taus=-0.5:0.5;
alpha=0.2;
stat = (s(N+1:2*N)).*exp(-j*pi*alpha*t(N+1:2*N));
shifted = conj(s(N+1-taus:2*N-taus)).*exp(j*pi*alpha*t(N+1-taus:2*N-taus));
prod=stat.*shifted.*exp(-2*j*pi*alpha*t(N+1:2*N));
caf2=(fft(prod));
thanks in advance
Ben, that code also does not run correctly:
>> caf2_2
Subscript indices must either be real positive integers or logicals.
Error in caf2_2 (line 11)
shifted = conj(s(N+1-taus:2*N-taus)).*exp(j*pi*alpha*t(N+1-taus:2*N-taus));
Is it running without errors on your system? I think you should at least make sure the code runs before sending it to someone else.
thanks mister but my code run without errors
caf2 not caf_2
Fs = 5000;
t = 0:1/Fs:1-1/Fs;
s = (cos(2*pi*600*t)+randn(size(t)));
N1=length(s);
N=floor(N1/3);
caf2 = zeros(2*N+1,N);
prods = zeros(2*N+1,N);
taus=-0.5:0.5;
alpha=0.2;
stat = (s(N+1:2*N)).*exp(-j*pi*alpha*t(N+1:2*N));
shifted = conj(s(N+1-taus:2*N-taus)).*exp(j*pi*alpha*t(N+1-taus:2*N-taus));
prod=stat.*shifted.*exp(-2*j*pi*alpha*t(N+1:2*N));
caf2=fftshift(fft(prod));
plot(abs(caf2))
The code you posted on April 4 produces the following output using MATLAB R2015b:
>> bm_code_040417
Subscript indices must either be real positive integers or logicals.
Error in bm_code_040417 (line 11)
shifted = conj(s(N+1-taus:2*N-taus)).*exp(j*pi*alpha*t(N+1-taus:2*N-taus));
The code you posted on April 7 produces the following output:
>> bm_code_040717
Subscript indices must either be real positive integers or logicals.
Error in bm_code_040717 (line 11)
shifted = conj(s(N+1-taus:2*N-taus)).*exp(j*pi*alpha*t(N+1-taus:2*N-taus));
I’m pretty sure the problem is with
taus=-0.5:0.5;
which yields
>> taus
taus =
-0.500000000000000 0.500000000000000
So you are mixing fractions with integers in your indexing.
This isn’t the kind of debugging I normally help with as it doesn’t have anything to do with understanding CSP.
I use rectangle pulse for BPSK. But the CAF shows followings: 1)there are only 3 lines (represent alpha=-2fc, 0, 2fc)when delay tau=0, and it do nothing with symbol rate; 2)CAF quickly decreases and tends to constant as delay increases when alpha is 2fc. Are those right? Why can’t find cycle frequencies related with symbol rate? Thanks in advance.
Did you use your own rectangular-pulse BPSK signal? What happens if you use the one I provided at the end of the post on rectangular-pulse BPSK? See the end of that post for details.
Thanks for your reply. After using your BPSK signal code, the CAF shows more peaks. But it’s still a big difference from your diagram. I have two questions here:
1) What is the CA formula of BPSK signal? I only find the cyclic spctrum formula in the book Statistical Spectral Analysis; 2) Should s[t] multiply by e^-j*pi*alpha*t before calculating delay product, like code written by Ben Mohamed aboved?
You can look at the references I cite for the formula for the cyclic autocorrelation for PSK/QAM (one of the references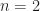 . That formula is slightly more general than the formula for the “symmetrical” cyclic autocorrelation. The symmetrical autocorrelation uses the lags
. That formula is slightly more general than the formula for the “symmetrical” cyclic autocorrelation. The symmetrical autocorrelation uses the lags  and
and  , whereas the formula (4) uses generic lags
, whereas the formula (4) uses generic lags  .
.
is my doctoral dissertation, which can be downloaded from the CSP Blog here). Or, look at formula (4) in the post on digital QAM and PSK. Specialize that formula to the case of
You don’t have to multiply by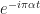 before averaging the lag product. You can either multiply the lag product by
before averaging the lag product. You can either multiply the lag product by 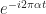 or multiply
or multiply 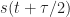 by
by 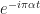 and
and 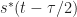 by
by 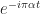 and then multiply them together.
and then multiply them together.
I suggest that you first try to get the cyclic autocorrelation correct for a single cycle frequency before you try to write code that computes the entire cyclic autocorrelation surface. I have seen many attempts at the latter that fail due to not understanding how to do the former. By the way, the surface I show in the post includes cyclic autocorrelation estimates for only those cycle frequencies that are known to exist for the rectangular-pulse BPSK signal I used.
Hi Chad!
You wrote in your blog https://cyclostationary.blog/2015/09/28/the-cyclic-autocorrelation-for-rectangular-pulse-bpsk/
“The non-conjugate CAF can be interpreted as the correlation between the lag product and the complex-valued sine wave ”.
Suppose I have a signal x1…x10.
I want to calculate the CAF for tau=2 and alf=0.1.
Then the calculations should be like this?
1. Lag product of the signal X for tau=2
x1 x2 x3 x4 x5 x6 x7 x8 .* conj(x3 x4 x5 x6 x7 x8 x9 x10)=
x1*conj(x3) x2* conj(x4) x3* conj(x5) x4* conj(x6) x5* conj(x7) x6* conj(x8) x7* conj(x9) x8* conj(x10)
2. Complex-valued sine wave
exp(2*pi*alf*t) t=0…7
e0 e1 e2 e3 e4 e5 e6 e7
3. Correlation between the lag product and the complex-valued sine wave
R(alf,tau)=R(0.1,2)=
= x1* conj(x3)*e0+x2* conj(x4)*e1+x3* conj(x5)*e2+x4* conj(x6)*e3+x5* conj(x7)*e4+x6* conj(x8)*e5+x7* conj(x9)*e6+ x8* conj(x10)*e7
Almost correct; you definitely have the right idea.
In Step 2, you’ll want a complex-valued exponential: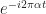 . (Don’t forget the minus sign and
. (Don’t forget the minus sign and 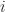 .)
.)
In Step 3, you’ll want to divide the sum by the number of elements that you have included. In this case .
.
I think you chose a signal having only ten samples to make the comment formatting easy, but just to be sure I need to say that you’ll need to average over longer durations for any signal of practical interest.
How averaging should be carried out?
Should one just take X long enough, for example, 1000
or, at the first stage, calculate the lag product for x1-x10, x11-x20, …, x991-x1000 and then average, getting the one vector of the lag product of 8 elements long?
The former is correct. Make sure your signal vector is long enough (pop-quiz: how?) and then use the method you wrote in your earlier comment with my slight modifications.
Each value of the lag product must be multiplied by a corresponding element of the complex sine wave to achieve the correlation between the lag product and the sine wave. If you take your long X vector and create a lag product and then average that, you’ll be destroying any sine-wave components (except for ) that might exist in the lag product.
) that might exist in the lag product.
Well, but I do not understand then what does your phrase mean in this blog:
“You don’t have to multiply by exp() BEFORE AVERAGING the lag product”.
And in your blog https://cyclostationary.blog/2015/09/28/the-cyclic-autocorrelation/ is equations 4 and 7. In equation 7, multiply by exponent is actually performed after averaging (E[…]).
Then how is it that the former is correct (just take X long)?
pop-quiz: how? – Determined by the required resolution Frequency and Cycle Frequency.
Where did you find the quote you made:
I mean, where did I write that?
Yes, if you could average over the ensemble using![E[\cdot]](https://s0.wp.com/latex.php?latex=E%5B%5Ccdot%5D&bg=ffffff&fg=1a1a1a&s=0&c=20201002) , then you could extract the cyclic autocorrelation from the resulting time-varying function through the Fourier-series operation.
, then you could extract the cyclic autocorrelation from the resulting time-varying function through the Fourier-series operation.
But your original question was about data , not an ensemble. Don’t forget Equation (8) in that post! That’s what you use on data.
, not an ensemble. Don’t forget Equation (8) in that post! That’s what you use on data.
Does that help?
https://cyclostationary.blog/2015/09/28/the-cyclic-autocorrelation-for-rectangular-pulse-bpsk/comment-page-1/#comment-1512
Thanks, yes it helped!
“I mean, where did I write that?”
https://cyclostationary.blog/2015/09/28/the-cyclic-autocorrelation-for-rectangular-pulse-bpsk/comment-page-1/#comment-1512
Thanks Serg! I see the problem now. The full quote is:
And the context was some code written by readers in which the input signal was multiplied by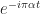 prior to forming the lag product. So what I said was a rather trivial observation that you can multiply the signal by an exponential related to
prior to forming the lag product. So what I said was a rather trivial observation that you can multiply the signal by an exponential related to 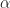 (and also multiply the conjugate by the appropriate exponential!), then form a lag product, then average. Or you can form the lag product, then multiply it by
(and also multiply the conjugate by the appropriate exponential!), then form a lag product, then average. Or you can form the lag product, then multiply it by 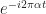 .
.
Hi Chad!
I realized simple model of the implementation of CAF and SCF.
The result is generally similar to that in your blog.
But there are a few problems.
1.For a single input (y_of_t = x_of_t1 + 0.0*x_of_t2+ n_of_t;), non-conjugate CAF and conjugate CAF match your results.
But if there are two input signals (y_of_t = x_of_t1 + 0.99*x_of_t2+ n_of_t;), then two signals are visible on the conjugate CAF, and only one on the conjugate CAF, that is, one signal is lost. Why?
2. Your non-conjugate SCF has a look that is different from my result (lagdot=x1.*conj(x2);).
And on the graph of the conjugate SCF (lagdot=x1.*(x2);), the cyclic frequency axis is digitized in the other direction (if without fliplr, fliplr(axis_alf)).
% CAF and CSP
clc
%% Initialize key variables.
T_bit = 10; % 1/T_bit is the bit rate
num_bits = 4000; % Desired number of bits in generated signal
fc1 = 0.05; % Desired carrier frequency(normalized units)
fc2=0.055;
N0_dB = 5.0; % Noise spectral density(average noise power)
%% Create the baseband signal.
% Create bit sequence.
bit_seq1 = randi([0 1], [1 num_bits]);
bit_seq2 = randi([0 1], [1 num_bits]);
% Create symbol sequence from bit sequence.
sym_seq1 = 2*bit_seq1 – 1;
zero_mat1 = zeros((T_bit – 1), num_bits);
sym_seq1 = [sym_seq1 ; zero_mat1];
sym_seq1 = reshape(sym_seq1, 1, T_bit*num_bits);
sym_seq2 = 2*bit_seq2 – 1;
zero_mat2 = zeros((T_bit – 1), num_bits);
sym_seq2 = [sym_seq2 ; zero_mat2];
sym_seq2 = reshape(sym_seq2, 1, T_bit*num_bits);
% Create pulse function.
p_of_t = ones(1, T_bit);
% Convolve bit sequence with pulse function.
s_of_t1 = filter(p_of_t, [1], sym_seq1);
s_of_t2 = filter(p_of_t, [1], sym_seq2);
%% Frequency-shift the baseband signal and add noise.
% Apply the carrier frequency.
e_vec1 = exp(sqrt(-1)*2*pi*fc1*[1:length(s_of_t1)]);
e_vec2 = exp(sqrt(-1)*2*pi*fc2*[1:length(s_of_t2)]);
x_of_t1 = s_of_t1 .* e_vec1;
x_of_t2 = s_of_t2 .* e_vec2;
% Add noise.
n_of_t = randn(size(x_of_t1)) + sqrt(-1)*randn(size(x_of_t1));
noise_power = var(n_of_t);
N0_linear = 10^(N0_dB/10);
pow_factor = sqrt(N0_linear / noise_power);
n_of_t = n_of_t * pow_factor;
y_of_t = x_of_t1 + 0.99*x_of_t2+ n_of_t;%!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=y_of_t;
Fs=1000000;
tau_max_t=15*10^-6;
tau_max_s=round(tau_max_t*Fs);
CAF=[];
for alf=0:1000:600000
alf
alfn=alf/Fs;
CAF1=[];
t=(1:length(x)-2*tau_max_s);
for tau=-tau_max_s:tau_max_s
x1=x(t+tau_max_s);
x2=x(t+tau+tau_max_s);
lagdot=x1.*conj(x2); % non-conjugate CAF
% lagdot=x1.*(x2); % conjugate CAF
ex=exp(-sqrt(-1)*2*pi*alfn*(0:length(lagdot)-1));
alftau=abs(sum(lagdot.*(ex))/length(lagdot));
CAF1=[CAF1 alftau];
end;
CAF=[CAF; CAF1]; % Cyclic Autocorrelation
end;
SCF=abs(fft(CAF’));
SCF=(fftshift(SCF)); % Spectral Correlation Function, Cyclic Wiener Relationship
axis_alf=[0:1000:600000];
axis_tau=[-tau_max_s:tau_max_s]/Fs;
bin=(Fs/length([-tau_max_s:tau_max_s]));
axis_freq=bin*[-tau_max_s:tau_max_s];
figure(1)
mesh(axis_tau, axis_alf, CAF)
figure(2)
mesh(fliplr(axis_alf), axis_freq, SCF)
Regarding Question 1, which is “Why are there two signals visible in the conjugate CAF but only a single signal in the non-conjugate CAF,” the reason is that you have generated two signals with the same bit rate but different carrier frequencies. Recall that for these BPSK signals, the non-conjugate cycle frequencies are harmonics of the bit rate. So here that means harmonics of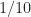 , or
, or  . For example, for
. For example, for 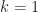 , each signal contributes its CAF for
, each signal contributes its CAF for 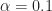 to the CAF for the data. For any two statistically independent signals
to the CAF for the data. For any two statistically independent signals  and
and  the sum signal
the sum signal 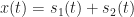 has a CAF or SCF that is the sum of the two individual CAFs or SCFs:
has a CAF or SCF that is the sum of the two individual CAFs or SCFs:
When only one signal possesses a particular cycle frequency, say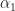 is possessed by
is possessed by  , then
, then
But if they both possess a cycle frequency, say , then the SCF of the sum signal is just the sum of the two SCFs (which may add constructively or destructively because they are complex-valued and depend on things like symbol-clock phase):
, then the SCF of the sum signal is just the sum of the two SCFs (which may add constructively or destructively because they are complex-valued and depend on things like symbol-clock phase):
Using the code you posted, I blindly estimated the non-conjugate and conjugate CFs for the sum signal using the SSCA:
Then I modified the code slightly so that the second BPSK signal has a different bit rate than the first. The first one still has a bit rate of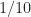 , but the second one has rate
, but the second one has rate 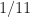 :
:
(I used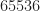 samples, so I had to increase the number of bits from
samples, so I had to increase the number of bits from 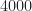 .)
.)
Regarding Question 2, I’m not sure what you mean by the reverse digitization of the cycle-frequency axis, but in most of my surface plots I tend to view the surface so that cycle frequency increases toward the viewer and spectral frequency increases to the left of the viewer. This is just for convenience and is a consequence of the fact that in the non-conjugate surface, the PSD is the largest slice and tends to block the view of the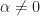 slices.
slices.
Thank you!
I apologize for the not entirely specific second question, but apart from digitizing the axis, there is a difference in the form of a SCF. You have (https://cyclostationary.files.wordpress.com/2015/02/ww_1.jpg) non-conjugate SCF is different from my non-conjugate SCF (alpha = 0.3 f = 0.1, and mine f = 0)
As you compute your estimates of the cyclic autocorrelation, you have decided to take their magnitude and store in a matrix:
alftau=abs(sum(lagdot.*(ex))/length(lagdot));
CAF1=[CAF1 alftau];
Later you take the Fourier transform of the obtained cyclic autocorrelation estimates, but remember that you are taking the Fourier transform of the magnitude (abs) of the estimates here. The phase information in the cyclic autocorrelation estimates is what leads to the frequency shift that you’re missing.
You’ll also need to be careful about transpositions once you restore the complex values:
SCF=abs(fft(CAF'));
And you might have a sign error in how you implement the delay:
for tau=-tau_max_s:tau_max_s
x1=x(t+tau_max_s);
x2=x(t+tau+tau_max_s);
Dear Prof. Spooner,
There is a typo in the begining of the post. There is “$100 + k 100$” text instead of latex rendering.
Fixed! Thank you very much Claudio!
Hi Dr. Spooner,
Been working on implementing a cyclic-autocorrelation function in MATLAB based on what I’ve read so far on your blog/papers!
While I believe the implementation is close because when alpha=0 it looks very similar to the plots you have in this article, when alpha is not 0 my plots look the same as when alpha=0. I’m assuming I’m either not implementing something correctly or I’m misunderstanding something about cyclic-autocorrelation. Can I email you the details of what I have so far to get help in learning what I’m misunderstanding?
Thank you,
John Snoap
Dr. Spooner,
Thank you so much for keeping this blog alive – it’s been a great help in learning about these techniques so far.
I was trying to implement the conjugate CAF function and it mostly looks like the graph you’ve produced above. However, the graph for each alpha in your example above appear to be strictly decreasing as alpha increases. Mine appear mirrored around alpha = 0.5, such that alphas = 0.4 & 0.6, 0.3 & 0.7, and 0.2 & 0.8 are identical.
Would you be able to provide any insight as to what I am doing wrong/differently? I am using the BPSK signal y_of_t as generated in your make_rect_bpsk.m file.
alphas = 0:0.1:0.8;
tau_lim = 15;
taus = -tau_lim:tau_lim;
Rx = zeros(length(alphas), length(taus));
for tau = taus
shifted = y_of_t(1 + abs(tau) : end);
unshift = y_of_t(1 : end – abs(tau));
len = length(shifted);
if tau > 0
comp_exp = e.^(-i * 2*pi * alphas’ * (tau : len + tau – 1));
else
comp_exp = e.^(-i * 2*pi * alphas’ * (0 : len – 1));
end
result = shifted .* conj(unshift) .* comp_exp;
% Integrate (sum), and convert asymmetrical to symmetrical CAF
Rx(:, 1+(tau+tau_lim)) = sum(result, 2) / len .* e.^(i*pi*alphas’*tau);
end
Rx = sqrt(Rx .* conj(Rx));
figure(1);
hold on;
for i = 1:length(alphas)
hp = plot3(alphas(i)*ones(size(taus)), taus, Rx(i, :));
set(hp, ‘linewidth’, 2);
end
view(3);
grid on;
xlabel(‘alpha’);
ylabel(‘tau’);
zlabel(‘Lin. Magnitude’);
Thanks for stopping by the CSP Blog, Stephen, and leaving a comment. I appreciate it.
My answer is that your straightforward time-domain estimator for the cyclic autocorrelation function requires that the signal is adequately sampled AND that the sine waves you use to multiply the delay product are adequately sampled. Once the cycle frequency is at 0.5 and above, the sine wave is ambiguous. I used a frequency-domain method to produce the cyclic autocorrelation estimates, and so sidestepped that problem. You can sidestep it in the time domain by increasing the sampling rate of the signal. You’ll always have the aliasing problem, but you’ll be able to fit more cycle frequencies in [0, 0.5] if the symbol interval is longer. Make sense?
Hi Dr. Spooner !
I’m trying to implement the example in the blog. The signal parameters are set as follows.
1) sampling frequency Fs=30kHz,
2) carrier frequency Fc=5kHz,
3) symbol rate Rsym=1k,
4) snr = 0 dB,
5) frequency resolution dα = Fs/65536=0.4578Hz,
6) estimated frequency range -10~10kHz,
7) delay resolution dτ=0.1ms or 1ms,
8) estimated delay range -20*dτ~20dτ.
Here is the simulation results https://imgur.com/gallery/agH7G8N.
I got different results when setting different values of delay resolution. I think the frequency resolution (i.e., dα) is related to the symbol rate since the cycle frequency is an integer multiple of symbol rate. The frequency resolution should be set much smaller than the symbol rate when estimating the CAF (am I right?). But how to set appropriate value of delay resolution and estimated delay range? Do you have any suggestion?
Looking forward to your reply!
Thanks very much for stopping by the CSP Blog and leaving a comment Tian!
I’m a bit confused by your set up; let me ask a few clarifying questions.
What method are you using to estimate the cyclic autocorrelation? Is it the inverse transform of a spectral correlation estimate, or a direct time-domain method?
Are you using a data-block length of 65536 samples? If so, then da = Fs/65536 is the cycle-frequency resolution, not the frequency resolution. How do you use the “estimated frequency range”?
In general, since you are using more-than-sufficient sampling for this narrowband signal, I wouldn’t worry about d$\latex \tau$. The resolution in the lag variable is simply equal to the sampling increment 1/Fs. In other words, once you’ve selected the parameters for simulating the signal, operate after that in the sample domain. The range of
is simply equal to the sampling increment 1/Fs. In other words, once you’ve selected the parameters for simulating the signal, operate after that in the sample domain. The range of  of interest here is determined by the properties of the simulated signal. For a rectangular-pulse BPSK signal with 30 samples per symbol, you’ll want to focus on the
of interest here is determined by the properties of the simulated signal. For a rectangular-pulse BPSK signal with 30 samples per symbol, you’ll want to focus on the  range of [-30, 30].
range of [-30, 30].
Hi Dr. Spooner!
Thank you for such a detailed answer. I referred to your blog [1] when calculating the CAF. And I also referred to the MATLAB code provided by msaserg when writing my own code. The CAF was estimated by equation (11) in [1] and actually implemented by FFT when programming (so it’s a direct time-domain method?). I think we don’t know the symbol rate of the received signal in the practical application. Hence, instead of only computing the cyclic autocorrelation at frequencies that are integer multiples of symbol rate, I calculated the cyclic autocorrelation function of all frequency points in the frequency range [0, Fs] (or [-Fs/2, Fs/2] if taking fftshift operation).
I’m sorry for confusing you. I need to correct some mistakes in my previous comment. Yes, you’re right! da = Fs/65536 is the cycle-frequency resolution. The estimated range of cycle-frequency is [-Fs/2, Fs/2] = -15~15kHz. The simulation figures provided in the link (https://imgur.com/gallery/agH7G8N) only plotted the CAF in the range of -10 ~10kHz. The entire signal included 4000 bpsk symbols, corresponding to 120000 samples. I intercepted a 65536-sample-length signal for analysis, and the amount of FFT points is also set to 65536.
I noticed that msaserg’s program only took individual delay values to estimate CAF, so I didn’t know how to set a proper delay resolution at first. Now I get it😀. As for the estimated delay range (Tau), dose it only need to cover twice the baseband pulse period? For example, for rectangular pulse shaping filter Tau=[-Fs/Rsym, Fs/Rsym], for SRRC pulse shaping filter, Tau is related to the truncated length or span symbols (refer to the parameter “span” in the rcosdesign function in MATLAB).
I upload my code to github (https://github.com/IanFreeman4/Cyclostationary-Signal-Processing). I’m not sure if the program is right, though the simulation results look similar to that in the blog.
Thanks again, Dr. Spooner. It’s really a great blog for CSP beginners!
[1] https://cyclostationary.blog/2015/09/28/the-cyclic-autocorrelation.
[T]ian:
Your rectangular-pulse BPSK plots look fine. The SRRC plot is OK, too, but I don’t know what the excess bandwidth is (roll-off parameter), so I can’t easily replicate. From the size of the symbol-rate peaks relative to the autocorrelation peak, it looks like the excess bandwidth is small.
Yes, I’d classify that as a direct time-domain method.
“frequency” –> “cycle frequency”
Sometimes you do know the cycle frequency in advance.
Since the SRRC signal is strictly bandlimited, its autocorrelation is infinite in duration. But of course it does decay rapidly enough. Your rule is a good rule-of-thumb though. If you look at the Gallery post for the cyclic autocorrelation, you can see that the cyclic autocorrelation for the SRRC signals have support that extends past that of a comparable rectangular-pulse signal.
Overall it looks like you are on the right track!
Dr. Spooner,
Thank you so much for keeping this blog alive – it’s been a great help so far.
I was trying to implement the CAF function and it mostly looks like the graph you’ve produced above. But I am still troubled by some questions:
First, My code:
x=y_of_t; %the y_of_t is the Bpsk Signal in your blog.
y=x;
alpha=2*pi/300;
max_tau=0;
R=cyclic_autocorrelation(x,alpha,max_tau);
y1=sqrt(R.*conj(R));
figure(1)
plot(y1);
figure(2)
mesh(y1);
%figure(4)
%mesh(y1)
function R=cyclic_cross_correlation(x,y,alpha,max_tau)
T=ceil(2*pi/alpha)-1;
lx=length(x);
t=0:lx-1;
R=zeros(max_tau*2+1,T+1);
for tau=-max_tau:2:max_tau
for k=0:T
R(tau+1+max_tau,k+1)=mean(x(1:lx-max_tau-tau).*y(max_tau+tau+1:lx) …
.*exp(-j*k*alpha*t(1+(max_tau+tau)/2:lx-(max_tau+tau)/2)));
end
end
% Compute odd time shift segments
t=t+0.5;
for tau=-max_tau+1:2:max_tau
for k=0:T
R(tau+1+max_tau,k+1)=mean(x(1:lx-tau-max_tau).*y(max_tau+tau+1:lx) …
.*exp(-j*k*alpha*t(1+(max_tau+tau-1)/2:lx-(max_tau+tau+1)/2)));
end
end
Then,my questions:
(1). When the max_tau=0, Why does the y1 value only exist when “alpha=30”? For the BPSK the bit rate is 10, so I expected that the y1 value will exist when x is an integer multiple of 10.
(2) When the max_tau=20, y1 Value only exists for the first half of the time lag? why?
(3) In addition, according to the Wiener Sinchin theorem, the corresponding spectral correlation function is equal to F{R(tau+1+max_tau,k+1)}, but the F{R(tau+1+max_tau,k+1)} and CSP Estimators(The Frequency-Smoothing Method) seem to have very different results, so which one more reliable?
Looking forward to your reply!
Your code does not run for several reasons. So I can’t understand or answer your questions.
1. Missing ‘end’ for the function.
2. Missing function ‘cyclic_autocorrelation.m’
3. Matrix dimension mismatch
Thanks for your reply.
x=y_of_t; %the y_of_t is the Bpsk Signal in your blog.
y=x;
alpha=2*pi/300;
max_tau=0;
R=cyclic_autocorrelation (x,alpha,max_tau); % lt’s wrong
%should be R=cyclic_cross_correlation(x,y,alpha,max_tau)
y1=sqrt(R.*conj(R));
figure(1)
plot(y1);
figure(2)
mesh(y1);
%figure(4)
%mesh(y1)
ps: R=cyclic_cross_correlation(x,y,alpha,max_tau) is a call function. This should work.
I had already substituted the cross function for the auto function when I showed you the error message.
Your code does not run to completion. The error messages depend on whether or not y_of_t is a row vector or a column vector. In one case I get the error I already showed you. In the other:
>> carl
Error using mesh (line 71)
Z must be a matrix, not a scalar or vector.
Error in carl (line 15)
mesh(y1);
If you want to post some working code sometime, I’ll take another look.
Hello,
nice blog but I want to ask how to achieve Rx(tau) for adding it in to (10) formula from The Cyclic Autocorrelation Function post. I try to do it in MATALB and here is my code for BPSK sig.
clc;
clear all;
%%%%%%%%%%%%
n_bit = 40;
Tbitu = 0.1;
%%%%%%%%%%%%%
Tvz = Tbitu/10;
Tcelk = n_bit*Tbitu;
time = 0:Tvz:Tcelk-Tvz;
freq = 0:1/(Tcelk-Tvz):1/Tvz;
%%%%%%%%%%%%
sekven = randi([0 1],[1 n_bit]);
amp_val = [];
for i = 1:length(sekven)
amp_val = [amp_val sekven(i).*ones(1,(Tcelk/Tvz)/n_bit)];
end
for i = 1:length(amp_val)
if amp_val(i) == 0
amp_val(i) = -1;
end
end
fcarr = (1/Tvz)/2;
carrier = exp(1j*2*pi*fcarr*time);
modulated = amp_val.*carrier;
Now I should shift signal (named modulated) in tau/2 which in this case would be:
tau = 1:length(time)/2;
t1 = (1:length(time)/2) + tau./2;
t2 = (1:length(time)/2) – tau./2;
???
and then I should just generate complex signal like
complex = exp(1j*2*pi*alpha*time);
with aplha = 0 and make sum of complex and Rx(tau) ???
Im new in this topic please, keep it simple as possible.
Thank you for your response.
Thanks for stopping by and leaving a comment Miropele! I appreciate it.
OK. Eq (10) from the Cyclic Autocorrelation post is a formula for the conjugate autocorrelation function, which is a time-varying function. I take it you want to find the cyclic autocorrelation functions that play the role of Fourier-series coefficients in (10).
I looked at the code you posted that generates the rectangular-pulse BPSK signal. You will have further difficulties if you stick with that code for the following two reasons: (1) the number of symbols is small, and (2) the carrier frequency you specify is 50 Hz (your sampling rate is 100 Hz). So this means you’ve shifted the BPSK signal all the way to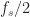 . The PSD looks like this:
. The PSD looks like this:
If you set fcarr = 0.1/Tvz, you get a carrier of 10 Hz, which has a more understandable and useful PSD that looks like this:
If you create the vectors t1 and t2 in this way, notice that some of their elements will not be integers. So if you try to use them to index your signal (‘modulated’), you’ll get errors because the indices to vectors in MATLAB have to be integers. You have to shift another way.
I suggest looking into MATLAB’s circshift.m function. You can circularly shift the data, then zero out the end to create a non-circular shift. That way you can create and
and  for even
for even  . But what about odd
. But what about odd  ? For that, you should look at the cyclic autocorrelation post again to understand the asymmetric version of the function.
? For that, you should look at the cyclic autocorrelation post again to understand the asymmetric version of the function.
Overall, my best advice to you at this point is to carefully read each of the comments my readers and I have made on the Cyclic Autocorrelation and Cyclic Autocorrelation for Rectangular-Pulse BPSK posts. I also strongly suggest you do all of your initial exploratory CSP work using a unit sampling frequency. You can add in the scaling effects of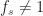 later, after you understand the estimators.
later, after you understand the estimators.
Hello again,
sorry for bothering you with my questions but I have another one. I tried to understand it again and this time I tried to make inverse FFT of spectral correlation function.so then I get cyclic autocorrelation function. In my opinion I have good result in spectral correlation function (in SCFtry variable). I also try to figure lack of sampels in my signals which you mentioned in you answear. The result of ifft is wrong and now I dont know what to do. Or is it easier to figure it in time domain which i tried to do previously? Thank you for your responde.
My code:
clc;
clear all;
%%%%%%%%%%%%
n_bit = 1000;
Tbitu = 0.01;
Fbitu = 1/Tbitu;
Tvz = Tbitu/10;
Fvz = 1/Tvz;
Tcelk = n_bit*Tbitu;
time = 0:Tvz:Tcelk-Tvz;
freq = 0:1/(Tcelk-Tvz):1/Tvz;
N_psd = 256;
Noverlap = 0;
%%%%%%%%%%%%
sekven = randi([0 1],[1 n_bit]);
amp_val = [];
for i = 1:length(sekven)
amp_val = [amp_val sekven(i).*ones(1,int32(Tcelk/Tvz)/n_bit)];
end
for i = 1:length(amp_val)
if amp_val(i) == 0
amp_val(i) = -1;
end
end
Fcarr = Fbitu;
carrier = exp(1j*2*pi*Fcarr*time);
modulated = amp_val.*carrier;
%%%%%%%%%%%%%%%%%%%%%%%%%
% figure(1);
% subplot(3,1,1)
% plot(time,amp_val);
% grid on;
% xlabel(‘t’);
% ylabel(‘A’);
% title(‘info sig’)
%
% subplot(3,1,2)
% plot(time,carrier);
% grid on;
% xlabel(‘t’);
% ylabel(‘A’);
% title(‘carrier sig’)
%
% subplot(3,1,3)
% plot(time,modulated);
% grid on;
% xlabel(‘t’);
% ylabel(‘A’);
% title(‘modulated sig’)
%%%%%%%%%%%%%%%%%%%%%%%%%
num_blocks = floor((length(amp_val)-Noverlap)/(N_psd-Noverlap));
Window = (rectwin(N_psd))’;
alpha = ((1:4)./Tbitu);
rilCPS = [];
for j = 1:length(alpha)
CPS = zeros(1,256);
index = 1:N_psd;
modulmin = amp_val.*exp(-1j*2*pi*(alpha(j)/2)*time);
modulplu = amp_val.*exp(1j*2*pi*(alpha(j)/2)*time);
for i=1:num_blocks
windowedminus = Window.*modulmin(index);
Ywmi = fft(windowedminus);
windowedplus = Window.*modulplu(index);
Ywpl = fft(windowedplus);
CPS = Ywpl.*conj(Ywmi) + CPS;
index = index + (N_psd – Noverlap);
end
rilCPS(j,:) = CPS;
end
SCFtry = 10*log10(fftshift(rilCPS));
freq_vec = linspace(-(max(alpha)/2),(max(alpha)/2),length(CPS));
figure(2);
plot(freq_vec, SCFtry);
legend(‘1/Tbitu’,’2/Tbitu’,’3/Tbitu’,’4/Tbitu’)
for i = 1:length(alpha)
lol(i,:) = ifft(SCFtry(i,:));
end
lol = fftshift(lol);
figure(3)
plot(freq_vec, lol);
Your main problem is that you are taking the inverse Fourier transform of the logarithm of the SCF estimate. You should be taking the inverse transform of the complex-valued estimate in rilCPS. You’ll see the expected cyclic autocorrelation shapes if you do that.
Also, you probably want to apply the 10*log10() to the absolute value of the SCF estimate and when you plot the cyclic autocorrelation at the very end, either plot its magnitude or plot the real and imag parts separately.
So am I right I have good results in SCF ? Because I did what you said and I think my results (with CAF) are vague. Sorry I dont know how to upload plot from matalb to comment.
sorry bad question … I figured it. Thank you for your patience. This blog is amazing.
Glad to help!
This shoud be right:
clc;
clear all;
%%%%%%%%%%%%
n_bit = 10000;
Tbitu = 0.1;
Fbitu = 1/Tbitu;
Tvz = Tbitu/10;
Fvz = 1/Tvz;
Tcelk = n_bit*Tbitu;
time = 0:Tvz:Tcelk-Tvz;
freq = 0:1/(Tcelk-Tvz):1/Tvz;
N_psd = 256;
Noverlap = 0;
%%%%%%%%%%%%
sekven = randi([0 1],[1 n_bit]);
amp_val = [];
for i = 1:length(sekven)
amp_val = [amp_val sekven(i).*ones(1,int32(Tcelk/Tvz)/n_bit)];
end
for i = 1:length(amp_val)
if amp_val(i) == 0
amp_val(i) = -1;
end
end
Fcarr = Fbitu;
carrier = exp(1j*2*pi*Fcarr*time);
modulated = amp_val.*carrier;
%[SCFtry,freq_vec] = SpecCorrFun(modulated,N_psd,Fcarr,Fvz);
num_blocks = floor(length(modulated) / N_psd);
S = modulated(1, 1:(N_psd*num_blocks));
S = reshape(S, N_psd, num_blocks);
I = fft(S);
I = I .* conj(I);
I = sum(I.’);
I = fftshift(I);
I = I /(num_blocks * N_psd);
I = 10*log10(I);
freq_c = [0:(N_psd-1)]/N_psd – 0.5;
figure(2);
plot(freq_c, I);
legend(‘1/Tbitu’,’2/Tbitu’,’3/Tbitu’,’4/Tbitu’)
title(‘SCF’)
%function [Isum,freq_c]=SpecCorrFun(signal,N_psd,Fcarr,Fvz)
num_blocks = floor(length(modulated) / N_psd);
alpha = ((0:0.1:0.5)./Tvz);
eS = modulated(1, 1:(N_psd*num_blocks));
for j = 1:length(alpha)
modulplu = eS.*exp(-1j*2*pi*(Fcarr-(alpha(j)))*time([1:length(eS)]));
modulplu = reshape(modulplu, N_psd, num_blocks);
S = reshape(eS, N_psd, num_blocks);
Y = fft(S);
X = fft(modulplu);
I = Y .* conj(X);
Isu(j,:) = sum(I.’);
Isum(j,:) = (fftshift(abs(Isu(j,:))));
end
CAFtry = [];
for i = 1:length(alpha)
CAFtry(i,:) = abs(fftshift(ifft(Isu(i,:))));
end
Isum = Isum /(num_blocks * N_psd);
Isum = 10*log10(Isum);
freq_c = [0:(N_psd-1)]/N_psd – 0.5;
figure(4)
plot(freq_c, CAFtry);
legend(string(alpha))
figure(3)
plot(freq_c, Isum);
legend(string(alpha))
The shapes of the cyclic autocorrelation functions appear to be correct, but the scaling is in question. The peak of the autocorrelation (non-conjugate cyclic autocorrelation for ) should be equal to the power of the signal giving rise to the autocorrelation.
) should be equal to the power of the signal giving rise to the autocorrelation.
I suggest you do the calculations and plots using a sampling rate of one to ensure all your scaling is right for that simpler case. Then introduce an arbitrary sampling rate.
Otherwise, it looks to me like you are on the right track!
Hello,
I think this should be right (CAF in aplha = 0 is equal to 1). Please I want to ask how to obtain information about baud rate from these results?
clc;
clear all;
%%%%%%%%%%%%
n_bit = 10000;
Tbitu = 0.01;
time = 0:1:n_bit-1;
freq = 0:1/(n_bit-1):1;
N_psd = 1024;
%%%%%%%%%%%%
sekven = randi([0 1],[1 1/Tbitu]);
amp_val = [];
for i = 1:length(sekven)
amp_val = [amp_val sekven(i).*ones(1,n_bit/(1/Tbitu))];
end
for i = 1:length(amp_val)
if amp_val(i) == 0
amp_val(i) = -1;
end
end
Fcarr = 1;
carrier = exp(1j*2*pi*Fcarr*time);
modulated = amp_val.*carrier;
Fvz = 1;
[Isum]=SpecCorrFun(modulated,time,N_psd,Fcarr);
[CAFtry]=CyclCorrFun(modulated,time,N_psd,Fcarr);
num_blocks = floor(length(modulated) / N_psd);
alpha = 0:0.125:0.5;
for j = 1:length(alpha)
Iabsft(j,:) = 10*log10(fftshift(abs(Isum(j,:))));
end
%Iabsft = 10*log10(Iabsft);
freq_c = [0:(N_psd-1)]/N_psd – 0.5;
[alko,tauco] = meshgrid(alpha,freq_c);
figure(3)
plot3(tauco,alko,Iabsft);
legend(string(alpha))
xlabel(‘\tau’)
ylabel(‘\alpha resp f’)
title(‘scf’)
figure(4)
plot3(tauco,alko,CAFtry);
legend(string(alpha))
title(‘caf’)
function [Iabsft]=SpecCorrFun(modulated,time,N_psd,Fcarr)
num_blocks = floor(length(modulated) / N_psd);
alpha = 0:0.125:0.5;
eS = modulated(1, 1:(N_psd*num_blocks));
for j = 1:length(alpha)
modulplu = eS.*exp(1j*2*pi*(Fcarr-(alpha(j)))*([1:length(eS)]));
modulplu = reshape(modulplu, N_psd, num_blocks);
S = reshape(eS, N_psd, num_blocks);
Y = fft(S);
X = fft(modulplu);
I = Y .* conj(X);
Isum(j,:) = sum(I.’);
Iabsft(j,:) = Isum(j,:) /(num_blocks * N_psd);
end
end
function [CAFtry]=CyclCorrFun(modulated,time,N_psd,Fcarr)
alpha = 0:0.125:0.5;
[Isum]=SpecCorrFun(modulated,time,N_psd,Fcarr);
CAFtry = [];
for i = 1:length(alpha)
CAFtry(i,:) = abs(fftshift(ifft(Isum(i,:))));
end
end
I don’t think you can do much with these results in general. You’ve fixed the cycle frequencies to values that don’t even match the cycle frequencies of the signal (k/8 vs. k/100).
If you have high SNR and your signal class is constrained, you can look at the autocorrelation function and get a good idea of what the symbol rate and carrier offset are by looking at the width of the function and the center point of the function, respectively.
If you are in a much more general setting, you don’t have those luxuries, and you have to perform a search. Even in the case above, you still have to perform a search, but the search space can be made smaller by using those rough parameter estimates.
So in general, you have to search over cycle frequencies somehow. See the SSCA and FAM posts, and their Comments sections.
Thank you for your perfect blog;
Also, I have a question; Would you please explain how we can calculate the estimated CAF “blindly” for our noisy rectangular-pulse BPSK signal? In another word how I can plot the Figure 1 and Figure 2 in this graph?
Hey Mahsa! Thanks for reading the CSP Blog and leaving a comment. Appreciated!
When I speak about blind estimation in CSP, I really mean ‘blind cycle-frequency estimation,’ because once you know the cycle frequencies for the data at hand, you can use one of several methods of non-blind estimation to find estimates of the spectral correlation function, cyclic autocorrelation function, spectral coherence, and higher-order cyclic temporal moments and cumulants.
In Figure 1, I ‘blindly estimate the CAF’ by blindly estimating the cycle frequencies, and then straightforwardly estimating the cyclic autocorrelation for each cycle-frequency estimate. In Figure 2, I simply know the cycle frequencies, and numerically evaluate the known cyclic autocorrelation formula for BPSK.
To blindly estimate cycle frequencies, you have several options. The best options in terms of computational cost are the strip spectral correlation analyzer (SSCA) and the FFT accumulation method (FAM). I suggest you read those posts, and especially study the comments made by CSP Blog readers, and myself, after you do so. I anticipate all your questions about blind estimation will be answered.
But … you can also use the time-smoothing method (TSM), frequency-smoothing method (FSM), “in a loop,” or use one of Antoni’s estimators. However, these all have inferior computational cost compared to the SSCA and FAM when you require a search over a cycle-frequency interval that is a substantial fraction of the sampling rate.
Lastly, the way I actually plot the functions is through MATLAB’s waterfall.m function.
Dr. Spooner,
In some examples (https://pysdr.org/content/cyclostationary.html, https://github.com/krono-i2/gr-CycloDSP) , the time shift of x(t) is performed via circular shift. Is this correct, or shift with loosing samples is more appropriate?
Welcome to the CSP Blog Ivan! And thanks much for the question.
I also use circular shifts to approximate a true time shift, especially in MATLAB. It would be more accurate to zero fill instead of circularly shift, but when the magnitude of the shift is very small compared to the data-block length that you are processing with SP or CSP, then I think the circular shift is a very good approximation. And, for me at least, that is almost always the case. The maximum autocorrelation or cyclic autocorrelation lag for which the function has significant magnitude is very small compared to a typical data-block length.
For the CSP-Blog mascot signal of rectangular-pulse BPSK with symbol rate 1/10 (normalized), the maximum significant lag has magnitude 10.