In a previous post, we introduced the frequency-smoothing method (FSM) of spectral correlation function (SCF) estimation. The FSM convolves a pulse-like smoothing window with the cyclic periodogram to form an estimate of the SCF. An advantage of the method is that is allows fine control over the spectral resolution of the SCF estimate through the choice of
, but the drawbacks are that it requires a Fourier transform as long as the data-record undergoing processing, and the convolution can be expensive. However, the expense of the convolution can be mitigated by using rectangular
.
In this post, we introduce the time-smoothing method (TSM) of SCF estimation. Instead of averaging (smoothing) the cyclic periodogram over spectral frequency, multiple cyclic periodograms are averaged over time. When the non-conjugate cycle frequency of zero is used, this method produces an estimate of the power spectral density, and is essentially the Bartlett spectrum estimation method. The TSM can be found in My Papers [6] (Eq. (54)), and other places in the literature.
The basic idea is to segment the provided data record into contiguous blocks of
samples each, compute the cyclic periodogram for each block, and average the results. Since we will likely use the FFT to compute the Fourier transform, we will be viewing each
-sample block as if its time samples correspond to
, and so the cyclic polyspectrum formula of My Papers [6] will have to be slightly modified to take into account the actual temporal start time for each block. This amounts to a phase compensation of each cyclic periodogram before it enters the averaging operation.
So let’s consider the Fourier transform (DFT) of a block of data that is shifted from the origin by some amount of time ,
The periodogram and cyclic periodogram are then functions of time offset as well,
and
and similarly for the conjugate cyclic periodogram. The TSM estimate of the SCF is simply the average value of the cyclic periodogram over all available values of ,
where is some pulse-like temporal window. In practice, the FFT is used to create each cyclic periodogram, so their relative phases are no longer taken into account. According to our Fourier transform result for a delayed signal, however, we can easily take this into account by multiplying each cyclic periodogram by
, where
represents the left edge (starting point) of the subblock. For blocks having length
samples, then, the value of
for the
th block is simply
. Our final TSM estimator expression is
where is just the cyclic periodogram created from the
th block of
samples using the FFT. Notice that when the cycle frequency is set to zero, the SCF estimate is an estimate of the PSD, and the TSM just averages
periodograms, as in the Bartlett spectrum estimation method. Here is the TSM (Bartlett) PSD estimate for our rectangular-pulse BPSK signal:

For this PSD estimate the data-record length is samples and the TSM block length is
samples, leading to
blocks. Recall that the bit rate for the BPSK signal is
and the carrier frequency is
(in normalized frequency units).
The TSM PSD estimate matches the FSM PSD estimate in the FSM post.
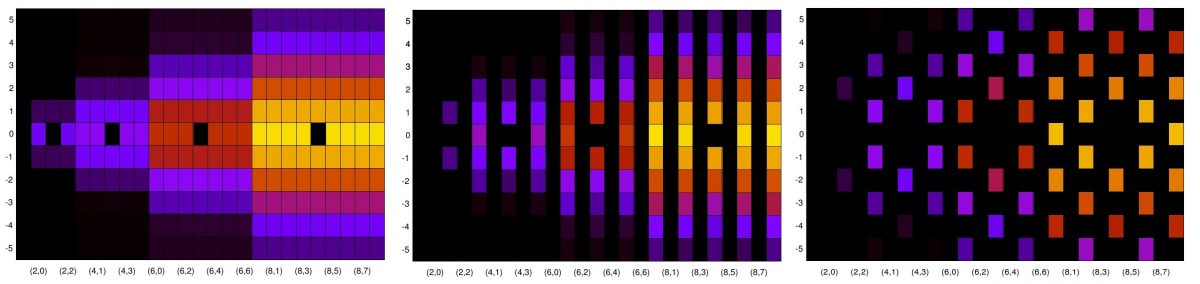
The TSM-based spectral correlation function estimates for the BPSK signal’s non-conjugate cycle frequencies are shown below:

and the conjugate-SCF estimates are:

Again, these TSM estimates match quite well with the FSM estimates.
The reason the TSM and FSM estimates match so well is that the temporal and spectral resolution parameters of the estimates are similar. For both methods, the temporal resolution is equal to the data-record length ( samples). For the FSM, the spectral resolution of the estimates is equal to the width of the frequency-smoothing window
, and for the TSM, the spectral resolution is equal to the intrinsic spectral resolution of each cyclic periodogram, which is equal to the reciprocal of the TSM block length (in normalized units), or
.
For the FSM results in the FSM post, the spectral resolution is Hz
points in
, and for the TSM results in this post, the spectral resolution is
Hz. The cycle-frequency resolutions for the two estimates are also the same at the reciprocal of the processed data-record length
. So the two estimates have comparable time, frequency, and cycle-frequency resolution parameters, and so produce similar results. The relationship between estimator quality and the temporal, spectral, and cycle-frequency resolutions is discussed in this post.
More on the TSM Phase-Compensation Factor
Some readers question the need for the phase-compensation factor in (5), which is given by
In fact it is not needed whenever it is always equal to a constant, such as one. This happens whenever the product is equal to an integer for all values of
. A sufficient condition is that the cycle frequency
is equal to a harmonic of
, that is,
. However, the phase factor is needed otherwise. Here are two confirming examples (do your own when you implement the TSM).
First, let’s look at the case where the cycle frequency is just the bit rate of our usual BPSK signal, or . Let’s pick the TSM block length
and process a total of
samples. We’ll plot the SCF estimate magnitude for the correct TSM and for the TSM without the phase-compensating factor:

In this case, for all integers
, and the phase-compensating factor is clearly needed.
On the other hand, consider a BPSK signal with bit rate and carrier
. Choose the bit-rate cycle frequency
, which is in fact equal to
for
:

And so in this case the phase-compensating factor is irrelevant since it is equal to one for all the TSM blocks, and the two TSM estimates are identical.
When using the TSM, you must calculate the conjugate cyclic periodogram by conjugate multiplication of the Fourier transform at offset +alpha/2 and -alpha/2.
Functionally, that seems to mean that you are multiplying the Fourier transform that has been circularly shifted left by 1 bin, by a conjugate circularly shifted right by 1 bin, to get the cyclic value at alpha = 2*Fs/N. You would circular shift by 2 bins to get alpha at 4*Fs/N, and so on all the way up to N bins, the maximum alpha shift at Fs.
Does that sound right? That means that including negative alpha values, the most alpha points will be N, and the max alpha value will be Fs, and the min alpha will therefore be 2*Fs/N?
Is there a way to get the alpha resolution (2*Fs/N) as fine as the frequency resolution (Fs/N) via some other mechanism? Do the FAM and SCCA algorithms have the same limitations on alpha?
Thank you for your blog and papers and time!
The conjugate cyclic periodogram is used to estimate the conjugate spectral correlation function and, unfortunately, it involves no conjugations. That is, the conjugate cyclic periodogram is X(f+a/2)X(a/2-f), whereas the (non-conjugate) cyclic periodogram goes like X(f+a/2)X*(f-a/2). So that is just terminology. I’m assuming that the rest of the comment is concerned with the non-conjugate cyclic periodogram and spectral correlation function.
Right.
You must use shifts that are equal to integer numbers of the FFT bins, yes, but there is nothing preventing you from using different shifts for the two involved shifted Fourier transforms. For example, you could form X(f + 1/N)X*(f). So that is a shift of one FFT bin for X(f + a/2) and no shift for X(f – a/2). This product ends up providing an estimate of S^b(g), where b = 1/N and g = f-1/N. So the minimum cycle frequency that you can look at (besides zero) is 1/N (or in your terminology Fs/N). Agree?
I’m working on a post on the three different kinds of resolutions involved in CSP (temporal, spectral, and cycle), but for now I think my comment above shows that the cycle resolution is Fs/N. Yes, this is equal to the native spectral resolution of the DFT using N points, but be careful because that is not the spectral resolution of the spectral correlation measurement in general. For the TSM, where we have N total samples and the FFTs have size M << N, the spectral resolution is 1/M (Fs/M in physical Hz). For the FSM, it is the width of the spectral smoothing window, which usually contains many of the N FFT points. For the SSCA, it is the reciprocal of the number of channels in the front-end channelizer.
It turns out the cycle resolution is always about equal to the reciprocal of the total number of samples processed, whereas the spectral resolution varies by estimator and is strongly affected by estimator parameters.
Great comments, aapocketz, thanks much.
I am having trouble understanding and implementing the delay needed to estimate the cyclic periodogram from the FFT. To start with, I am not completely sure whether I understand the need for it. I take that the idea behind this is to actually estimate the band-pass zero centered signals from the FFT bins in the spectrogram, but I am not sure of why this is needed (the covariance should cancel out this delay as it is the same for the two signals). Furthermore, I’ve been testing my implementation and with/without the delay compensation results seem fairly similar (if any, the version without the delay seems slightly better). It may be that the signal length I am using is big enough to “average out” the delay effects, but I have not been able to find a case where the delay compensed option is significantly better (I take I may have an error on my own implementation).
Any insight that you can provide?
Thanks and really incredible job with this blog.
Thanks for your interest Pablo!
What is the TSM block length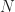 in samples, and what are the cycle frequencies
in samples, and what are the cycle frequencies 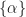 that you are passing to the TSM (normalized frequencies)?
that you are passing to the TSM (normalized frequencies)?
Because this phase-compensating factor has historically been met with confusion and resistance, I’m working on an addendum to the TSM post… I’m hoping to be much more clear about it than I’ve been in the past. Sorry about that!
I’ve been playing around with different values and signals. Using your BPSK signal and the values given in the post (N = 256, etc), I’ve been able to reconstruct something similar to your plots, both with no phase-compensation and with my maybe incorrect one. With respect to the cycle frequencies, I am generating the complete square matrix (every combination of spectral correlation). For the delay compensation I am using normalized frequencies (alpha = [0, 1/256, 2/256, … 255/256]) and multiples of N for D, i.e: [0, 256, 512, …] up to the last segment. I understand that this delay does not change between spectral components (FFT bins). Not sure if this gives you an idea of where my mistake is. If you have any reference I can use to better understand the phase compensation, I am willing to read it.
Even with my likely ill-formed SCF I have been able to see some interesting features of different modulations, this is a really interesting topic.
Thanks a lot!
Let’s say you are processing a total of samples, and your TSM block size is
samples, and your TSM block size is 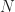 samples. Recalling the basics of cycle-frequency resolution, cycle frequencies separated by about
samples. Recalling the basics of cycle-frequency resolution, cycle frequencies separated by about 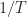 will be distinguishable. So a full spectral correlation analysis must consider the cycle frequencies
will be distinguishable. So a full spectral correlation analysis must consider the cycle frequencies 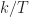 ,
,  . If you consider instead the set of cycle frequencies
. If you consider instead the set of cycle frequencies  ,
, 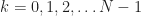 , you will be missing a lot of cycle frequencies (more and more as
, you will be missing a lot of cycle frequencies (more and more as  increases with
increases with 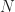 fixed). In either case, the phase-compensating factor will be one for all cycle frequencies and all block indices if both
fixed). In either case, the phase-compensating factor will be one for all cycle frequencies and all block indices if both 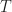 and
and 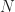 are dyadic (powers of two).
are dyadic (powers of two).
More to the point, what happens with your two versions (one with my phase correction, one without) when you use my rectangular-pulse BPSK signal as an input and you specify the single cycle frequency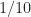 (which is the bit rate of the rectangular-pulse BPSK signal)? Here the cycle frequency is not the reciprocal of a dyadic number. For my TSM implementations, only the one with the phase-compensator works.
(which is the bit rate of the rectangular-pulse BPSK signal)? Here the cycle frequency is not the reciprocal of a dyadic number. For my TSM implementations, only the one with the phase-compensator works.
I now see where my mistake was. I thought I was using N=256, but actually, I was using N=100, so 1/10 was one of the values generated. This way, the delay compensation plays no role, and so the estimation held up without delay compensation. Changing to N=256, the delay compensation is indeed needed and works as expected.
Thanks a lot for your support. I will keep on digging in these concepts!
Quick question: 1) “The spectral resolution is 0.005 Hz (164 points in g(f))”.. would it actually be 1/164 which is 0.0061 or do you take the RMS bandwidth which in the case of rectangular window would match the support?
Thanks
Masoud: Thanks for visiting the CSP Blog and leaving a comment!
In the FSM post example, I mentioned that the processing block length is 32768 samples. That means each FFT bin would represent 1/32768 Hz (normalized frequencies here). And therefore the samples in the cyclic periodogram are separated by that same amount, 1/32768 Hz. If the smoothing window width is 164 frequency samples, the spectral resolution of the smoothed cyclic periodogram is therefore 164/32768 = 0.005 Hz. I also mention using zero-padding in the FSM post. To maintain an effective spectral resolution of 0.005 Hz, the number of points in the smoothing window in that case is 328 because the FFT bin width is then 1/65536.
So in this case where you are zero padding to increase it’s length to 65536, what will be cycle frequency resolution be based on the tsm post that follows – 1/NM ?
So 1/65536 or will it still be 1/32768 ?
Thanks for this amazing blog… very informative
The spectral and cycle-frequency resolutions do not change with the introduction of zero padding. The effect of zero padding is to interpolate–you get some points in a transform, say, between the points that you got without zero padding.
I advocate some zero padding in spectral correlation estimators such as the frequency-smoothing method (FSM) and the time-smoothing method because it makes the selection of the FFT bins corresponding to the up and down frequency shifts (of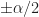 ) more accurate–the choices render the product of shifted discrete Fourier transforms closer to what would have been obtained in continuous time.
) more accurate–the choices render the product of shifted discrete Fourier transforms closer to what would have been obtained in continuous time.
So the resolution properties of the measurement don’t change, but the accuracy of the spectral correlation estimates, as a function of frequency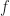 , for some chosen cycle frequency
, for some chosen cycle frequency 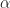 improve a little. There’s no magic–you don’t get a huge gain.
improve a little. There’s no magic–you don’t get a huge gain.
In the TSM, zero padding takes place for each of the many short Fourier transforms that are used to create the many short cyclic periodograms, which are phase compensated and averaged to yield the final spectral correlation estimate.
If zero padding could substantially improve the resolution of a frequency-domain measurement, such as the frequency of a sine wave using the Fourier transform, you could just take a couple points of the sine wave and apply vast padding and get a highly accurate frequency estimate. But you can’t, and I think the reason comes from the mathematical operation involved in computing the transform, which is a correlation between the data and a sine wave. That, in turn, can be viewed as a convolution, and the transfer function of the corresponding filter will depend on the duration of the data over which the data is non-zero, not just the transform length.
Thanks, the zero padding makes sense to me now. One thing I noticed when I added in the zero padding:
To recreate the FSM method estimates for SCF, we started off with a signal of length 32768.
We zero pad this signal to increase it’s length to 65536
We compute the cyclic periodogram by shifting X(f) by alpha/2 to left and right, conjugate and multiply. Here X(f) is the N point FFT and N in this case is 65536. Finally we divide by N (Eq: 8)
When I divide by N = 32768, my plot match exactly with what you have on the FSM post.
But when I divide by N = 65536 the PSD values are slightly lower. I am right to assume the division factor N should be the length of the signal before zero padding?
Question2: To compute the conjugate SCF, we need to multiply X(f + alpha/2) by X(alpha/2 – f)
What method are you or the others on this blog using to compute this term X(alpha/2 – f)
I have tried multiple ways in the time and freq domain, reversing X(f) to X(-f) but I can’t get the plots to match your output. What method are you or the others on this blog using to compute this term?
The PSD for the latter case should be shifted downward by exactly 3 dB:
Why?
Note that by adding 32768 zeros to the end of the 32768 BPSK-plus-noise samples, we obtain a vector that is twice as long as the original signal vector, but the energy of that new vector is exactly the same as before, since adding up the squares of all those zeros is still just adding zero. Energy is unchanged.
Now, power is energy per unit time, or in calculations, computed energy divided by the length of time over which that energy was computed. Therefore, the total power of the padded signal should be half that of the original signal.
So when you go to divide the periodogram’s Fourier-transform product by the padded length, and smooth correctly, you get a PSD whose integral will equal half the power of the original signal, as it should, since the padded signal has half as much power.
If you want to focus on the power of the original signal, it is perfectly fine to divide the periodogram’s product by the length of the original signal. Or you could just use a generic PSD estimator that only knows the length of its input vector, and outside of a call to that PSD estimator scale the PSD by the padding factor.
So the short answer to your Question 1 is: “It’s up to you.”
For Question 2, how to create the frequency-reversed and -shifted Fourier transform for use in computing the conjugate spectral correlation function, what programming language do you use? I use C and MATLAB (I have FSM, TSM, SSCA, etc., implementations in both languages). In the MATLAB case, first try to create
-shifted Fourier transform for use in computing the conjugate spectral correlation function, what programming language do you use? I use C and MATLAB (I have FSM, TSM, SSCA, etc., implementations in both languages). In the MATLAB case, first try to create  (
( ). How might you do that? (Hint: use fliplr.m or the vector-index-reversal notation like X(end:-1:1).)
). How might you do that? (Hint: use fliplr.m or the vector-index-reversal notation like X(end:-1:1).)
Not sure why the reply button doesn’t exist to your latest post, but I can confirm that after zero padding the PSD for the latter case is exactly 3 dB below !!
I am using python and numpy to compute the conjugate SCF. I reversed X(f) to get X(-f) using the [::-1] for the alpha = 0 case. I am able to get the correct output.
Now from X(-f) to get X(-f + alpha) I perform the following: I first compute X(-f) and then I shift by alpha/2
alphas = [0.1, 0.2, 0]
scf_array = np.zeros((len(alphas), len(signal)), dtype=np.complex64)
for i, alpha in enumerate(alphas):
offset = int(np.round(alpha / 2 * len(signal)))
freq_scf, dft_daniel_scf = np.fft.fftfreq(len(signal), d=1), np.fft.fft(signal, n=len(signal))
freq_scf = np.fft.fftshift(freq_scf)
dft_daniel_scf = np.fft.fftshift(dft_daniel_scf)
dft_up = np.roll(dft_daniel_scf, offset)
dft_down = np.roll(dft_daniel_scf, -offset)
cyclic_periodogram = (dft_up * np.conj(dft_down)) / len(signal)
cyclic_periodogram_conj = (dft_up * np.roll(dft_daniel_scf[::-1], offset))/len(signal)
scf = np.convolve(cyclic_periodogram_conj, g, mode=’same’)
scf_array[i, :] = scf*2
Another strategy is to realize that and so first create
and so first create  then reverse that. The advantage is you already know you correctly create
then reverse that. The advantage is you already know you correctly create  .
.
Apologies, it was a beginner error on my path. I was reversing and shifting the wrong frequency term.
This was due to having misinterpreted the left and right shift freq components.
Glad you found it! I’ve done the same thing…
While studying your post on time smoothing and the need for the phase compensation factor where we average blocks of data to compute the cyclic periodogram, can we obtain an estimate of the original IQ samples by applying inverse fft?
Say for example, we start with 1024 samples of complex IQ data. Using the time smoothing method described in your post, we set N = 256, M = 4 and alpha = 0 (PSD).
Now, we compute the cyclic periodogram for the 4 blocks of IQ data using a N = 256 point fft.
Then compute the SCF by applying the phase compensation factor and dividing by M = 4.
Above, we have started with 1024 points of complex data in the time domain and at the end of eq. 5 from the time smoothing post, we have 256 points of complex data in the frequency domain.
Using ifft, will I be able to estimate the original 1024 points from the 256 points obtained in eq. 5 ?
The real world use case of this would be something like:
Collect 1024 million samples of data which I know is a BPSK signal.
I detect my signal center freq and bw, symbol rate etc. using the CSP techniques you describe.
Compute the SCF. From 1024 million samples I am down to say 256K samples. Now I want to demodulate.
Storing millions of IQ samples for demod takes up a lot of space compared to storing only a few hundred samples of SCF complex data. So I can delete the IQ samples after performing the SCF. Only when I need to do a demod, I can use ifft and obtain an original estimate.
Is there any other advantage of this process besides saving space ?
No, you cannot form an SCF estimate (including the special case of the PSD), and then use that to “get back” to the original data.
Creating the SCF requires averaging, and that is an irreversible process. If I tell you thirty students took an exam, and the average was 74, can you tell me the thirty scores?
Moreover, in the example above, where you set , you do indeed destroy the phase of the data. A simple proof of this consists of computing the periodogram (you have specified
, you do indeed destroy the phase of the data. A simple proof of this consists of computing the periodogram (you have specified  ) for a complex sine wave such as the one in Eq (3) in the Three Resolutions post. The phase of that sine wave is
) for a complex sine wave such as the one in Eq (3) in the Three Resolutions post. The phase of that sine wave is 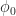 . But the periodogram Eq (16) does not depend on
. But the periodogram Eq (16) does not depend on 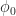 . Another way of saying this is that an infinite number of distinct sine waves (indexed by
. Another way of saying this is that an infinite number of distinct sine waves (indexed by 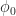 ) map to the exact same periodogram. Therefore the periodogram cannot be reverse-mapped to a unique sine-wave input.
) map to the exact same periodogram. Therefore the periodogram cannot be reverse-mapped to a unique sine-wave input.
So although the TSM does save you memory, because you never need to store and transform a long vector of complex numbers, it cannot be used as a prelude to demodulation. Once you compute any estimate of the SCF, CAF, coherence, cyclic cumulants, etc., you have discarded the specific sequence of student scores, as it were, that lead to the estimate.
Note also that if you *did* compute an estimate of the SCF, and then applied an inverse FFT to that estimate, you’d just get an estimate of the cyclic autocorrelation function, since the CAF and SCF are a Fourier-transform pair.
Many times I have shown a complicated SCF surface corresponding to an I/Q input containing multiple spectrally overlapping signals, and a person would see the separation of the features in the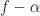 plane and, quite understandably, would want to connect that separation of features into somehow separating the signals themselves. To separate the signals requires a lot of detailed work–see my FRESH filtering post.
plane and, quite understandably, would want to connect that separation of features into somehow separating the signals themselves. To separate the signals requires a lot of detailed work–see my FRESH filtering post.
Another question about the phase correction term. It seems that I am having issues to align the cyclic periodogram whenever the expected cyclic frequency does not exactly fall on a frequency bin of the FFT. I am using a QPSK signal at 10Hz carrier and 1.25Hz symbol rate. My FFT has 600points which gives me a resolution of 0.1Hz. with my implementation, the cyclic frequencies at k*2.5Hz are all properly estimated while the frequencies at (2*k-1)*1.25Hz are all zero.
Looking at the real and imaginary parts of each cyclic periodograms clearly shows an energy peak on the two closest FFT bins (e.g. at 1.2Hz and1.3Hz, 3.7Hz and 3.8Hz) however the phase of these peaks are not aligned, and the average in [equ(5)] makes those peaks vanish. On the other hand, averaging the absolute value of the cyclic periodograms (instead of the real and imaginary parts individually as per [equ (5)]) clearly show peaks at the expected location.
For probably the same reason, using an FFT of 602 samples (instead of 600) makes all spectral correlation peaks disappear (except at \alpha=0 of course). Using the average of the absolute value (instead of the average of the real/imaginary parts) shows strong peaks at the expected locations.
Do you think this a normal behavior, or do you suspect that I have an issue with my implementation? Any advice would be highly appreciated.
Thank you for your all the dedication on the work you have been doing with this blog and papers.
Thanks for stopping by, Arnaud! All signs point to an error in the phase-correction term that you apply. You didn’t include a description of that term, so I can’t say for sure that it is wrong. Your description implies that the sampling rate is 60 Hz, and your QPSK signal has 48 samples per symbol. So, the even harmonics of the symbol rate are cycle frequencies that contain an integer number of FFT bins (for TSM FFT length of 600), and the odd ones don’t. Since you get good SCF estimation (I assume “the cyclic frequencies … are all properly estimated …” means that the SCF is properly estimated, not the CFs) for even harmonics of the symbol rate, I suspect that your applied phase-compensation factor is always one.
No, this is not normal behavior. Exactly what is your phase-compensation factor?
Chad, thank you very much for your reply.
You are right the sampling frequency is indeed 60Hz.
Given the cyclic periodogram I^\alpha (j, f), where \alpha is the non-normalized cyclic frequency, and f the non-normalized frequency [f=fs*(0:(Nfft-1))/Nfft] (fs is the sampling frequency and Nfft is the size of the FFT vector).
I obtain the periodogram by multiplying the column vector FFT by its conjugate transpose (non-conjugate periodogram). The resulting “matrix” [X(f1)*conj(transpose(X(f2)))]_m,n has a frequency and cyclic frequency given by f_m,n=f1_m/2+f2_n/2 and \alpha_m,n=f1_m-f2_n.
The phase correction term I am using is exp(-2*i*pi*\alpha/fs*offset(j)), where offset(j) is the starting point (i.e. index value) of the jth cyclic periodogram block. Since \alpha is not normalized in my implementation, I need to divide it by the sampling frequency to make it consistent with equ5.
So you are using the outer product of the FFT with itself to obtain a matrix that contains several cyclic periodograms. The main diagonal is the conventional periodogram. The off diagonals are the cyclic periodograms. Agree?
Your description of the phase compensation term is ambiguous. The matrix you obtain contains multiple cyclic periodogram values, and so each value of the matrix will require its own compensation term, which is related to the particular value of cycle frequency for the value. That is, there is no single phase compensation term for you. I can’t tell from your description whether you are applying the correct term to each individual matrix element or are applying a single compensation term to the entire matrix.
I recommend that you first code and debug a single-cycle-frequency TSM algorithm. Make sure that it works for arbitrary TSM block lengths and arbitrary cycle frequencies. That is, the cycle frequencies that are implied by your outer product are a small subset of the possible cycle frequencies.
“So you are using the outer product of the FFT with itself to obtain a matrix that contains several cyclic periodograms. The main diagonal is the conventional periodogram. The off diagonals are the cyclic periodograms. Agree?”
Yes, this is exactly what I have been doing.
“I can’t tell from your description whether you are applying the correct term to each individual matrix element or are applying a single compensation term to the entire matrix.”
I am using a different compensation term for each individual matrix element. If I_m,n(j) is the jth “periodograms matrix” obtained from the outer product of the jth FFT vector, the compensation term I am using for the element _m,n (i.e. row m, column n) is exp(-2*i*pi*\alpha_m,n/fs*offset(j))
“I recommend that you first code and debug a single-cycle-frequency TSM algorithm. Make sure that it works for arbitrary TSM block lengths and arbitrary cycle frequencies.”
Thank you for the recommendation. I will try to implement the TSM for a single frequency and follow up if I have some more issue.
Thank you again for the helpful feedback.
Your blog and information is fantastic. I’m confused by something here though, and it’s pretty basic. Apologies.
In (1) you define the DFT in a way I’ve never seen that seems odd to me. The DFT definition is usually agnostic to sampling rate, and even if you normalize such that your sampling interval is 1 the DFT equation should be the same. Except your definition does not normalize the numerator of the exponent term by N. Even for normalized sampling rates shouldn’t the numerator be (-i 2 pi f t / N)?
Okay, I think I see what’s going on. It seems to me there are *two* normalizations here:
1. Ignore actual sample rate and pretend our data is sampled on 1 second intervals.
2. The DFT is defined such that the output frequency isn’t indexed like a normal DFT but defined on the interval [0, (N-1)/N], or simplified a bit, [0, 1).
Of course, that might work well for showing the math and equations. If I’m using an actual computer to compute the DFT I’m going to have sampled indices on number 2 above. But I think I can get there. I’m just running into issues with the phase normalization term. When I try to apply it “as is” (with alpha being the baud in Hz divided by the actual sample rate) it’s not working. So I’m guessing there’s something in this DFT definition here that will explain my troubles.
Thanks for stopping by the CSP Blog cubingthesphere! And for the comments.
Well, I am indeed hiding the exact values of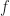 in (1). The usual way of defining
in (1). The usual way of defining 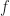 in the DFT is as MATLAB does:
in the DFT is as MATLAB does: 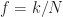 for
for  :
:
But engineers like to see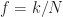 for
for  , so MATLAB provides fftshift.m.
, so MATLAB provides fftshift.m.
In other words, in my (1), time (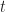 and
and  ) are integers, which is consistent with a unit sample rate, but
) are integers, which is consistent with a unit sample rate, but 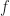 is a value like
is a value like  , the exact nature of
, the exact nature of  is up to you. Mathematicians typically like the MATLAB definition, electrical engineers like the alternative definition (supplied by fftshift.m acting on the output of fft.m in MATLAB).
is up to you. Mathematicians typically like the MATLAB definition, electrical engineers like the alternative definition (supplied by fftshift.m acting on the output of fft.m in MATLAB).
Yes, and this is pervasive at the CSP Blog. See my lengthy recent post on the sampling rate for a discussion (scroll down to near the end if you don’t want the tutorial).
Well, I’m hiding the indexing. Perhaps I shouldn’t have done that. The TSM will work for whatever you use for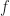 , as long as it is consistent from TSM block to TSM block.
, as long as it is consistent from TSM block to TSM block.
Well… see above. The choice is yours. ‘To fftshift or not to fftshift, that is the question!’
I doubt that the definition of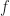 is your problem. Here are some TSM estimates for the rectangular-pulse BPSK signal using the TSM except I just removed all fftshifts:
is your problem. Here are some TSM estimates for the rectangular-pulse BPSK signal using the TSM except I just removed all fftshifts:
What do you think?
Thanks for the reply!
You’re right, that wasn’t my issue. I noticed an error with which leg I was conjugating. Well, or I could change the sign on the phase term. Either way that seemed to be my problem. Thanks for the explanation.