Update to the exchange: May 7, 2021. May 14, 2021.
Reader Clint posed a great question about zero-padding in the frequency-smoothing method (FSM) of spectral correlation function estimation. The question prompted some pondering on my part, and I went ahead and did some experiments with the FSM to illustrate my response to Clint. The exchange with Clint (ongoing!) was deep and detailed enough that I thought it deserved to be seen by other CSP-Blog readers. One of the problems with developing material, or refining explanations, in the Comments sections of the CSP Blog is that these sections are not nearly as visible in the navigation tools featured on the Blog as are the Posts and Pages.
I mentioned zero-padding in the FSM post, and Clint asked about it. Here is his original comment:
Hi Chad,
You’ve mentioned zero-padding the signal in at least a couple places, such as above:
“When the two frequencies do not correspond to multiples of 1/N, then zero-padding the data prior to FSM estimation is advisable; this will allow a closer match to discrete frequencies.”Is there a reason to use zero-padding rather than just to process a longer signal in the first place? In your example above, why don’t you just generate a signal that is twice as long (or whatever length you want to achieve with zero-padding)? Or, if working with a real signal, just process/record a longer chunk? Unless you’re using a custom FFT implementation, it’ll still require the same amount of computation.
I could see it being beneficial in hardware or real-time applications, where you could shortcut part of the calculations if you know large chunks are zeros. But, as you say, many such applications will do better with the TSM anyway.
Thanks!
Clint
I replied thusly:
Thought-provoking question Clint! Thanks. Let’s see if my reply is convincing.
Is there a reason to use zero-padding rather than just to process a longer signal in the first place?
If we want to do the best CSP we can with the data block we have, with length , then we cannot increase the data length. We always want to do the best we can with what we have, for sure, but we are also sometimes constrained by short data records, and so do not have the choice you suggest.
The problem, as we agree I think, is that the number of FFT bins represented by the frequency is not an integer. So we have to pick two frequency bins that best represent, in some sense, the frequency span
. Suppose that
lies exactly between two FFT bins. That is
, where
is some integer between
and
. Then, yes, if we were to process with a new block length of
, the frequency distance of
would then be an integer. But what about when the number
is not exactly halfway (or quarter-way, eighth-way, etc.) between FFT bins? Such as a number like
. This number cannot be represented as
for any
and
. In fact, this is why I’ve chosen the bit rate of the rectangular-pulse BPSK signal used throughout the CSP Blog to be
–it is not friendly to DFTs of sequences with dyadic lengths
. (Don’t want to sneak in some numbers with special privileges or properties…) When
is near the midpoint between FFT bins, we can increase
and it will be closer to an integer number of bins, as you suggest. But further increases may find it farther away again. If we look at
for a variety of
we get:
1024 51.2
2048 102.4
4096 204.8
… 409.6
… 819.2
… 1638.4
… 3276.8
… 6553.6
… 13107.2
… 26214.4
2^20 52428.8
So whether the frequency is close to an integer number of bins depends on the number of bins, and it doesn’t converge.
What is important is whether the accuracy of the representation of in terms of some integer number of FFT bins is small or larger relative to the inherent cycle-frequency resolution of the measurement, which is about
. The resolution of the measurement doesn’t change when we add zeros–we are just interpolating by zero padding. But by doing that interpolation, we allow the approximation of
by an integer number of FFT bins to be more accurate, yet we do not have the problem of finer resolution that we would have if we increased the data length. So we get more accurate results with the same data.
Moreover, increasing the data-block length to better represent one cycle frequency can result in a worse representation for another cycle frequency exhibited by the data. Zero-padding helps them all, or at least does no harm (if, say the cycle frequencies really are of the form ).
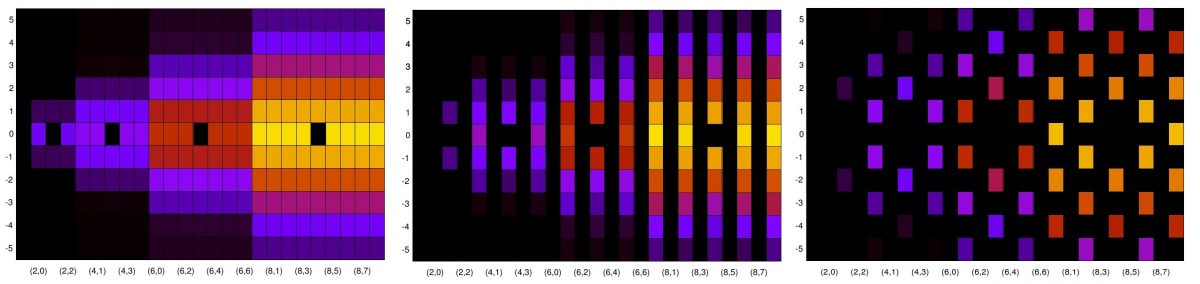
Here is my offered evidence. (This was worth doing because I think we all struggle with this problem in the CSP community.) Sticking with our old friend the rectangular-pulse BPSK signal with bit rate , carrier offset of
, unit power, and noise with
dB, we can plot the peak spectral correlation and spectral coherence magnitudes for a particular implementation of the FSM and a variety of block lengths
. First the spectral correlation:

Next the coherence:

Notice that the cycle frequency of is unaffected by either zero padding. That is because that cycle frequency is always perfectly represented by an integer number of FFT bins. The others are affected though.
What do you say?
You can find the rest of the exchange in the Comments section of the FSM post.
h/t Reader Clint.
Hi Chad,
I experimented with ways to automatically pad my signals with the minimum number of zeros such that alpha/2 lands on an integer number of bins.
Provided alpha is a rational number a = p/q in simplest form, then (I think) the signal length N should be a multiple of LCM(p, 2q)/p. Since p and q are coprime, either N has to be a multiple of q (when p is even) or 2q (when p is odd). So I just round N up to the nearest multiple. This seems to be working well so far.
Does this make sense to you? I’m not sure if Clint or somebody else mentioned this already.
It makes sense to me mathematically. I’m not sure about how practical it is. If you are in the non-blind situation, you know at least one cycle frequency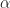 , and so you can determine
, and so you can determine  and
and  in advance. But what happens when
in advance. But what happens when  is large? Then a multiple of
is large? Then a multiple of  or
or  might exceed the data length you’re willing or able to process. If you are doing something with multiple cycle frequencies, the padding might be (probably will be) different for the different cycle frequencies.
might exceed the data length you’re willing or able to process. If you are doing something with multiple cycle frequencies, the padding might be (probably will be) different for the different cycle frequencies.
In controlled simulation land, often we pick cycle frequencies with small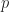 and
and  and all will be easy. But remember that the apparent cycle frequency in the real world is a function of the transmitted cycle frequency and the exact sampling rate you’re using (and the Doppler shift if you’re looking at conjugate cycle frequencies), so who knows what
and all will be easy. But remember that the apparent cycle frequency in the real world is a function of the transmitted cycle frequency and the exact sampling rate you’re using (and the Doppler shift if you’re looking at conjugate cycle frequencies), so who knows what 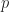 and
and  are until you’re doing the processing. I suppose you could force an approximation to the true
are until you’re doing the processing. I suppose you could force an approximation to the true 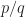 with a ceiling on their values. But I typically stick with a simple padding factor of two or four for all cycle frequencies.
with a ceiling on their values. But I typically stick with a simple padding factor of two or four for all cycle frequencies.