In this post I describe a basic estimator for the spectral correlation function (SCF): the frequency-smoothing method (FSM). The FSM is a way to estimate the SCF for a single value of cycle frequency. Recall from the basic theory of the cyclic autocorrelation and SCF that the SCF is obtained by infinite-time averaging of the cyclic periodogram or by infinitesimal-resolution frequency averaging of the cyclic periodogram. The FSM is merely a finite-time/finite-resolution approximation to the SCF definition.
One place the FSM can be found is in (My Papers [6]), where I introduce time-smoothed and frequency-smoothed higher-order cyclic periodograms as estimators of the cyclic polyspectrum. When the cyclic polyspectrum order is set to , the cyclic polyspectrum becomes the spectral correlation function, so the FSM discussed in this post is just a special case of the more general estimator in [6, Section VI.B].
Let’s start by reviewing the FSM for power-spectrum measurement. That is, let’s begin by looking at an estimator for the power spectral density (PSD). We’ll use discrete time and discrete frequencies in this post, in contrast to My Papers [6], because almost everybody who might read this post will be interested in sampled data. Moreover, discrete frequencies lead to discrete cycle frequencies in the method, which causes a significant complication in practice. We’ll highlight that complication, and show how it can be mitigated.
The Frequency-Smoothed Periodogram
The power spectrum estimate is obtained by smoothing the periodogram. The discrete Fourier transform (DFT) of is defined by
where for
. The periodogram is the normalized squared magnitude of the DFT,
The periodogram is not a particularly good spectrum estimator when the data is random; it is quite useful when the data is nonrandom and contains periodic components. The maximum-likelihood estimator for the frequency of a tone in white Gaussian noise is the location of the maximum of the Fourier transform magnitude over all frequencies , which is usefully approximated by the discrete-time/discrete-frequency periodogram. For random data (like communication signals), the periodogram is erratic and does not converge to the true PSD even as
.
The PSD can be accurately estimated by smoothing the periodogram,
where is some unit-area pulse-like function, such as a rectangle. The smoothing implied by this convolution allows the estimate to converge to a biased (distorted) estimate of the true PSD. If
is large and the width of
is small relative to the fluctuations over frequency in the true PSD, then the bias is low and the estimator converges to very nearly the true PSD. More explicitly, the FSM for PSD estimation is
for . So to implement this FSM, we need only use an FFT algorithm and a general convolution algorithm capable of handling complex inputs. An FSM-based PSD estimate for our rectangular-pulse BPSK signal is shown here:

This estimate is formed from a data record with length samples and a rectangular smoothing window
with width
frequency bins, which is about
(normalized) Hz.
The frequency-smoothed periodogram method of spectrum estimation is referred to as the Daniell method after P. J. Daniell (The Literature [R42]).
The Frequency-Smoothed Cyclic Periodogram
For the spectral correlation function, we modify the FSM for the PSD
by replacing the periodogram with the cyclic periodogram, which is defined
by
where is a cycle frequency of interest. Since
is a discrete-frequency function, the arguments
are valid only if
. That is, the discrete-frequency function
can be shifted to the left and right only by multiples of the discrete frequency
. It may happen that the true cycle frequency does not satisfy this constraint. In practice, the closest discrete shifts are chosen for
. When the two frequencies do not correspond to multiples of
, then zero-padding the data prior to FSM estimation is advisable; this will allow a closer match to discrete frequencies. In general, the
and
shifts don’t have to be negatives of each other. The idea is to choose the shifts
and
such that
is minimized (My Papers [16]).
To estimate the SCF, then, we convolve the cyclic periodogram with a smoothing window as before,
for . All that is required to implement this algorithm is an FFT, complex multiplication, and a general convolution algorithm (such as MATLAB’s conv.m or filter.m). The conjugate SCF is estimated by frequency smoothing the conjugate cyclic periodogram given by
Applying this algorithm to our rectangular-pulse BPSK signal, we obtain the following estimates for the non-conjugate SCF:

The conjugate SCF estimates are:

To obtain these estimates, we used a data-record length of samples and a rectangular
with width
frequency points, or about
Hz. Recall the sampling frequency is set to unity here, the signal’s bit rate is
, and the carrier frequency is
. The
-sample data record is zero-padded by a factor of two prior to forming the cyclic periodogram.
The estimates presented in Figures 2 and 3 closely match the known exact formulas for the non-conjugate and conjugate spectral correlation functions for rectangular-pulse BPSK, as illustrated in the second-order verification post.
Choice for the Frequency-Smoothing Window 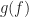
We used the rectangular pulse in our estimator examples for a good reason: computational cost. For arbitrary
, a general-purpose convolution routine can be used to find the SCF estimate, but the convolutions can be expensive. Computational cost can be reduced by selecting only a subset of all possible output frequencies, and computing the convolution just for those particular spectral frequencies.
Arbitrary output frequencies can be accommodated, however, by using a rectangular smoothing window because the convolution can be efficiently performed by a running sum over the cyclic periodogram. The estimates for successive spectral frequencies can be obtained by subtracting the cyclic-periodogram value that is no longer covered by the support of
(left edge of the window) and adding the one that is newly included in the support (right edge of the window).
In the final analysis, the FSM offers good control over spectral resolution, but requires an FFT operation on the entire data record. When the signal of interest has low signal-to-interference-and-noise ratio (SINR), the required data-record length can be very large. For non-real-time CSP applications running on modern general-purpose computers, this isn’t usually a problem. But when attempting to transition CSP to hardware, long complex-valued data vectors are problematic. For such cases, we can turn to the time-smoothing method (TSM) of SCF estimation, which we discuss in another post.

Hey! This is a great blog! Learning a lot here. Can you please provide MATLAB codes to generate these plots?
Thanks!
Thanks AN. The CSP Blog is a self-help blog. I don’t give out much code. Let me know if you get stuck, though, trying to write your own. That’s the only way you’ll really understand CSP.
Hi Chad
I think you chose complex-valued waveform of BPSK signal to estimate the PSD and cyclic spectrum, right?
And how can I judge the simulation results of the FSM priodogram and cyclic priodogram of BPSK signal correct or not?
The value range of n in Equation (10) can not reach 0 and N. The reason is that for certain cycle frequency, “n+a1=0” , right?
Yes, the BPSK signal I use throughout the CSP Blog is complex-valued.
Do you mean how can you judge whether my plots are correct? Or your plots? My plots are consistent with theory in the cases where I know the theory, such as PSK and QAM signals. So you can use my plots in the BPSK posts (here and here) or the gallery posts (here and here) to compare with yours.
Yes, when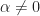 in the non-conjugate SCF, you cannot use all the indices in the sum over
in the non-conjugate SCF, you cannot use all the indices in the sum over  unless you are willing to view the FFT output
unless you are willing to view the FFT output  as a periodic function (with period
as a periodic function (with period 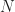 ). But generally you don’t want to do that, and the edges of the cyclic periodogram will contain zeros. The larger
). But generally you don’t want to do that, and the edges of the cyclic periodogram will contain zeros. The larger 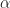 becomes, the more zeros you’ll see at the ends (this also corresponds to the diamond shape of the support for the SCF).
becomes, the more zeros you’ll see at the ends (this also corresponds to the diamond shape of the support for the SCF).
But why the estimation performance of FSM method decreased as I increased the length of data record? The simulation parameters I chose were the same as yours.
It isn’t possible to substantively answer this question. Not enough information!
Hi Chad
According to the equation (25) in Gardner’s paper “Measurement of Spectral Correlation”, I think the result of equation (3) should be divided by the frequency bins number of smoothing window. Do as what I advised, the FSM-based PSD matches well with the theoretical PSD for BPSK signal.
What about your opinion?
My (3) is a bit more general than Gardner’s (25), which smooths using a unit-area rectangle. My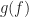 can be any pulse-like unit-area window function, but I do use a rectangle a lot too. The factor you say is missing is actually embedded in the definition of
can be any pulse-like unit-area window function, but I do use a rectangle a lot too. The factor you say is missing is actually embedded in the definition of 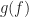 : It has unit area. Therefore if it is a rectangle, it has height equal to the reciprocal of the width. I’ve added “unit area” to the post to clarify.
: It has unit area. Therefore if it is a rectangle, it has height equal to the reciprocal of the width. I’ve added “unit area” to the post to clarify.
The Figure 1 in this post is similar to what your code make_rect_bpsk.m. But you did not use the convolution after the FFT, but the plot looks same.
So my question is related to this: To estimate the SCF, we should take the FFT of non conjugate CAF and then we need to convolve this with a smoothing window g(f). Does it give any extra benefit of using the g(f)? What is a good size of g(f)?
Is the FFT of non conjugate CAF called the cyclic Periodogram?
I don’t quite understand this. The plot in Figure 1 looks the same as what?
No, to estimate the SCF, take the FFT of the data, shift it up and down by , multiply, divide by the length of the data, then convolve the result with a smoothing window. See the posts on the frequency-smoothing and time-smoothing methods of spectral correlation estimation for details and examples.
, multiply, divide by the length of the data, then convolve the result with a smoothing window. See the posts on the frequency-smoothing and time-smoothing methods of spectral correlation estimation for details and examples.
Yes. The main point of the Periodogram post is that if you don’t average (“smooth”) the periodogram in either time or frequency, you will have a highly erratic function of frequency. Note also that the reliability (variance) of a spectral correlation estimate is inversely proportional to the product of the data-block length and the frequency resolution. For the frequency-smoothing method, the frequency resolution is the width of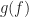 . So, to generate a reliable (low variance) estimate, you want to use large data-block lengths and large (coarse) frequency resolution (wide
. So, to generate a reliable (low variance) estimate, you want to use large data-block lengths and large (coarse) frequency resolution (wide 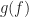 ).
).
A good width for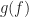 is typically 1-5% of the sampling rate.
is typically 1-5% of the sampling rate.
No. The cyclic periodogram is defined in (3) and (5) in the Periodogram post. The Fourier transform of the non-conjugate CAF is the non-conjugate spectral correlation function.
Thanks for the reply. I meant, the Figure 1 in this post is similar to what your code make_rect_bpsk.m. generates.
Thanks for the reply. I need some more clarification. You said “To estimate the SCF, take the FFT of the data, shift it up and down by \alpha/2, multiply, divide by the length of the data”.
1. Shift it up and down by alpha/2: Is it not giving back the same matrix if I shift it up by alpha/2 and then down by the same amount. Also is this shifting the same what fftshift does? If not same, then what this shift up and down by alpha/2 is doing here?
2. Then you said “multiply”: what do I multiply with what? I understood the divide by the length of the data.
3. Is the cyclic periodogram calculated as: FT[x(t)*exp(j*2*pi*alpha/2*t)] * conj{FT[x(t)*exp(-j*2*pi*alpha/2*t)]}
Well, you shift the FFT up by to get
to get 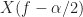 and shift it down by
and shift it down by  to get
to get  . Those are the two quantities you need to multiply together to get the cyclic periodogram.
. Those are the two quantities you need to multiply together to get the cyclic periodogram.
No. MATLAB’s fftshift.m swaps the second half of a vector for the first half: fftshift([1 2 3 4]) = [3 4 1 2]. This is identical to circshift([1 2 3 4], 2). The shifting we need to do in CSP depends on the value of the cycle frequency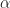 .
.
The mathematics of CSP says that you can estimate the spectral correlation function by averaging the cyclic periodogram, which is the product of two frequency-shifted Fourier transforms. More physically, the spectral correlation function is the temporal correlation between two narrowband spectral components of a signal, after those components have been isolated and frequency-shifted to zero frequency. And those two frequency components have frequencies specified by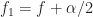 and
and 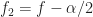 in the usual parameterization.
in the usual parameterization.
See answer to Question 1 above.
I’m not sure about the plus and minus signs in the exp() functions, and you’ll need to divide by length(x(t)), but, yes, this is one way to obtain the cyclic periodogram. I typically don’t use this method, because if you’re careful, you can do the frequency shifting in the frequency domain using only things like circshift.m, which is much cheaper than creating the complex sine waves and multiplying them by the signal x(t) and taking two (not one) Fourier transforms.
I find an interesting phenomenon. To meet the condition that the approximated value, obtained by integrating PSD values over frequency and multiplying that sum by the frequency increment, must be equal to the estimate of power. Therefore, different PSD estimating methods have different frequency increment and different PSD value. For example, periodogram based PSD values are much greater than that based on TSM and FSM method.
How do you explain that phenomenon?
Yes, the different methods can have different frequency-bin increments as well as different spectral resolutions. This means that for any particular given frequency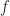 , the PSD estimates from the various methods will likely have different values. But for properly set up measurements (the measurement spectral resolution is well-matched to the data’s spectral characteristics, the data-block length is sufficient to allow averaging away erratic components), the values will be quite similar, as you can see from my comparisons between the FSM and TSM outputs.
, the PSD estimates from the various methods will likely have different values. But for properly set up measurements (the measurement spectral resolution is well-matched to the data’s spectral characteristics, the data-block length is sufficient to allow averaging away erratic components), the values will be quite similar, as you can see from my comparisons between the FSM and TSM outputs.
And the sum of the PSD estimate values, multiplied by the frequency increment, should be very close for each method.
Yes, the periodogram is highly erratic, and is a terrible estimator of the PSD, so there will be periodogram values that are very much greater than the true PSD value and periodogram values that are very much less than the true PSD value–that’s why we need the averaging.
Convolving the periodogram of x(t) with g(f) would obtain PSD estimate with length of N+164-1. So what is the frequency increment between the adjacent frequency bins of that PSD estimates? Is the frequency increment fs/(N+164-1)?
This is a convolution question, not a CSP question! The spacing between the samples does not change as a result of convolution.
The posts are very helpful for the beginners like me. It would be better if you supply more detailed unit labels on the figures. I think the unit of the nomalized frequency is [cycle/sample], and of the PSD is [dB/(rad/sample)]. I am not sure whether the units I added here is correct? Or maybe it is a traditional label manner in the CPS society.
Thanks for visiting the CSP Blog and leaving a comment Smoon! I appreciate it.
I agree with you about normalized frequency–strictly speaking I should label axes with [Cycles/Sample] or the like. But when the actual physical sampling rate really is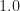 , then the unit is also Cycles/Second, or Hz. Mostly I’m following convention, which is to use ‘Hz’ for both physical frequency and normalized frequency. To translate any frequency axis from normalized frequency to physical frequency, just multiply by the actual sampling rate.
, then the unit is also Cycles/Second, or Hz. Mostly I’m following convention, which is to use ‘Hz’ for both physical frequency and normalized frequency. To translate any frequency axis from normalized frequency to physical frequency, just multiply by the actual sampling rate.
And yes, the physical unit of a power spectrum is Watts/Hz. Normally expressed in decibels, but often in decibels relative to some basic power level, such as one Watt (dBW) or 1 milli Watt (dBm). In almost all of my posts, I’m unconcerned with the actual power level of the data–even when I capture data using my lab equipment I don’t keep track of the relationship between the integers I obtain from a sampler and the power level of the electromagnetic wave incident on the attached antenna. So I rather lazily just use decibels and the relationship to actual physical power is suppressed.
What is the ‘CPS society’?
This feels like a dumb question, but I’m completely failing to re-create your plots for the conjugate SCF. (Using what should be identical to your textbook BPSK signal example.)
I have another function that calls the function below and convolves a smoothing window with the result. The results match your FSM plots quite well for the non-conjugate SCF, but not for the conjugate version.
I’ve tried computing the SCF for all possible values of alpha for the signal under consideration, and none of the results match your plot for the conjugate SCF; in fact, they’re all pretty noisy and remain below 0dB.
I’ve also implemented the time-smoothing method, and I can replicate your plots for the non-conjugate SCF, but again not for the conjugate SCF. (I still have a bug somewhere such that my phase compensation factor only works when alpha*N is an integer, but I’m working on fixing my frequency-smoothed conjugate SCF before going back to that.)
Below is my python function computing the cyclic periodogram; my understanding is that the only difference is whether X2 should have the conjugate operation applied (yes for the non-conjugate SCF, no for the conjugate SCF).
def cyclic_periodogram(x, alpha=0, conjugate=False):
“””Compute the cyclic periodogram from the given signal x
I^A(f) = 1/N * X(f + alpha/2) * conj(X(f – alpha/2))
where X(f) is the Fourier transform of x(n) and x(n) has N total samples
Assumes that alpha is in normalized frequency; i.e. alpha = alpha_absolute/sampling_frequency
Note that the conjugate cyclic periodogram does not include the conjugation operation in its definition:
I^A_*(f) = 1/N * X(f + alpha/2) * X(f – alpha/2)
“””
X = numpy.fft.fftshift(numpy.fft.fft(x))
# shift X left by # of bins corresponding to alpha/2 and another copy right by the same amount
# eventually can slightly improve the resolution by allowing slightly different left/right shifts
offset = int(numpy.round(alpha/2 * len(X)))
X1 = numpy.roll(X, offset)
X2 = numpy.roll(X, -offset)
if not conjugate:
X2 = numpy.conj(X2)
print(f’Computing non-conjugate cyclic periodogram for alpha = {alpha}, offset = {offset}’)
else:
print(f’Computing conjugate cyclic periodogram for alpha = {alpha}, offset = {offset}’)
return 1/len(X) * X1 * X2
Can you see something I’m missing here? Except for the conjugation of X2 (and the values of alpha where the SCF is meaningful), all my code is identical for the non-conjugate and conjugate SCF, and it matches your plots perfectly for the non-conjugate case.
Thanks for any help!
Ugh, it got rid of all the indentation, making it much less readable. I’ll clarify if needed…
To clarify one point, – when I tried to estimate the conjugate SCF for “all possible values of alpha” I did reduce the total length from 32,768 to 4,096 samples. My understanding is that that should just increase the variance of the resulting SCF estimate, but shouldn’t fundamentally change the behavior.
Also, there’s raw LaTeX in this post, as well as the post for the TSM.
Thanks very much for pointing out the raw latex! Fixed it.
Yes, reducing the amount of processed data does increase the variance of the estimate, and also impacts the all-important cycle-frequency resolution parameter. Which means that one may also experience cycle leakage when the block length is too small–energy from a nearby slice of the spectral correlation function can leak into the slice you are focusing on. So, variance and leakage are both increased in general.
Hey Clint! Sorry about the loss of the indentation when you posted your code. When I comment on a comment, I have several markup tool buttons available, including “code,” which allows posting of code that should be formatted reasonably by WordPress. Do you see that when you comment?
One major problem you are having is your statement:
That is not the only difference; see Equation (11) in the FSM post and Equation (8) in the SCF post. Instead of the non-conjugate cyclic periodogram
you remove the conjugate and negate the argument of the second factor
Try implementing that and re-running the estimates.
Thanks for clarifying, Chad, in spite of my apparent inability to read equations.
I don’t see any formatting/markup options when commenting; just raw text.
I don’t have it working yet, although I have something implemented that at least corrects for the problem you mentioned, as well as limiting the domain of the SCF by padding with zeros beyond f = +/-0.5 (my previous code treated the X(t, f) as being infinitely periodic in frequency, though I came across this comment – https://cyclostationary.blog/2018/06/01/csp-estimators-the-fft-accumulation-method/#comment-2131 – which makes me think that you had a discussion of that with plots of the SCF domain elsewhere, though I can’t remember where at this point. Is there a way to view a list of all blog posts, instead of either searching (and hoping I stumble upon the right term) or viewing the archives a month at a time? (Those are the only options I’ve found, other than just going through articles sequentially.)
I haven’t yet published a post on the spectral correlation “principal domain,” but I may have a plot or two showing the diamond or part of it. Perhaps in the SSCA post.
I’ve created a new page for the CSP Blog. Look at the top of the home page for “All CSP Blog Posts” and click that to get a simple list, in chronological order, of all posts. Is that what you were looking for? Once I hear back from you about whether or not that is what you desired, and perhaps suggestions for improvement, I’ll do a little post announcing it. You aren’t the first to suggest the navigation on the site is cumbersome.
Thanks Clint!
Thanks for the new page, Chad! It’s definitely helpful, and a good complement to the posts you already had with beginner links and category links.
The only additional suggestion I might have would be a list of all tags, but that would be somewhat redundant with the list of categories, and thus much less useful.
Got to work on this some more today. Finally got it working!
Turns out the remaining problem was an off-by-one error in the indexing for the conjugate SCF case. Now I just need to look at it in more detail to be sure of _why_ the indexing needs to be the way it is.
Thanks again for the help Chad!
In case it helps others trying to implement this, I’ll describe what I was seeing before I found my bug.
My problematic curves were generally the same shape as Chad’s, but 10-15dB lower and they had fairly high variance/noise. After thinking about cycle leakage, I wondered if my offset was close but not quite right, which turned out to be the case.
Consistent with Chad’s comments above about cycle leakage and block length, the level of my curves went down as I increased the total length of random data that I was processing.
Hi, thank you for creating this blog. Can you confirm that the parameter m (appearing below eq. 7 and eq. 10) is the width of the rectangle used for smoothing. Thanks.
Thanks for the comment, Ada, and for checking out the CSP Blog.
Here is what I say near (10):
The parameter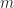 here is an integer-valued index that specifies a frequency. Since we’re doing digital signal processing here, the input signal is a sampled function of time, and the FFT and SCF are discrete-frequency functions. So
here is an integer-valued index that specifies a frequency. Since we’re doing digital signal processing here, the input signal is a sampled function of time, and the FFT and SCF are discrete-frequency functions. So 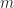 just tells us which frequencies we are getting out of the FSM algorithm.
just tells us which frequencies we are getting out of the FSM algorithm.
The width of the rectangle or, more generally, the width of the smoothing function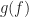 is usually referred to as
is usually referred to as 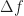 in the CSP Blog. In the examples in the FSM post, the width of
in the CSP Blog. In the examples in the FSM post, the width of 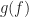 is
is 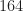 frequency bins, or
frequency bins, or 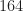 consecutive values of
consecutive values of 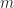 .
.
Does that help?
Hello, thank you for your fast response. So the smoothing function g(f) will comprise 164 frequency values of n for averaging. The convolution will use m as an index for the shifting. This means that the output of the FSM will be about 200 averaged points (32768/164) when no overlapping of the smoothing function is used. I do not understand what you mean by the width of g(f) is 164 consecutive values of m ? Thanks.
I see you posted a comment after this one indicating you understand after all. For others, I’ll just say here that width of the smoothing function is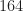 points, so for each output spectral correlation estimate (one value of spectral frequency
points, so for each output spectral correlation estimate (one value of spectral frequency 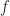 ),
), 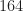 values of the cyclic periodogram are averaged together, not
values of the cyclic periodogram are averaged together, not 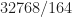 .
.
Hello, I understood it. Thank you !
Hi Chad,
You’ve mentioned zero-padding the signal in at least a couple places, such as above:
“When the two frequencies do not correspond to multiples of 1/N, then zero-padding the data prior to FSM estimation is advisable; this will allow a closer match to discrete frequencies.”
Is there a reason to use zero-padding rather than just to process a longer signal in the first place? In your example above, why don’t you just generate a signal that is twice as long (or whatever length you want to achieve with zero-padding)? Or, if working with a real signal, just process/record a longer chunk? Unless you’re using a custom FFT implementation, it’ll still require the same amount of computation.
I could see it being beneficial in hardware or real-time applications, where you could shortcut part of the calculations if you know large chunks are zeros. But, as you say, many such applications will do better with the TSM anyway.
Thanks!
Clint
Thought-provoking question Clint! Thanks. Let’s see if my reply is convincing.
If we want to do the best CSP we can with the data block we have, with length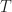 , then we cannot increase the data length. We always want to do the best we can with what we have, for sure, but we are also sometimes constrained by short data records, and so do not have the choice you suggest.
, then we cannot increase the data length. We always want to do the best we can with what we have, for sure, but we are also sometimes constrained by short data records, and so do not have the choice you suggest.
The problem, as we agree I think, is that the number of FFT bins represented by the frequency is not an integer. So we have to pick two frequency bins that best represent, in some sense, the frequency span
is not an integer. So we have to pick two frequency bins that best represent, in some sense, the frequency span  . Suppose that
. Suppose that  lies exactly between two FFT bins. That is
lies exactly between two FFT bins. That is  , where
, where  is some integer between
is some integer between  and
and 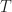 . Then, yes, if we were to process with a new block length of
. Then, yes, if we were to process with a new block length of  , the frequency distance of
, the frequency distance of  would then be an integer. But what about when the number
would then be an integer. But what about when the number  is not exactly halfway (or quarter-way, eighth-way, etc.) between FFT bins? Such as a number like
is not exactly halfway (or quarter-way, eighth-way, etc.) between FFT bins? Such as a number like 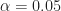 . This number cannot be represented as
. This number cannot be represented as 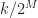 for any
for any  and
and 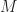 . In fact, this is why I’ve chosen the bit rate of the rectangular-pulse BPSK signal used throughout the CSP Blog to be
. In fact, this is why I’ve chosen the bit rate of the rectangular-pulse BPSK signal used throughout the CSP Blog to be 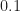 –it is not friendly to DFTs of sequences with dyadic lengths
–it is not friendly to DFTs of sequences with dyadic lengths 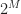 . (Don’t want to sneak in some numbers with special privileges or properties…) When
. (Don’t want to sneak in some numbers with special privileges or properties…) When 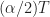 is near the midpoint between FFT bins, we can increase
is near the midpoint between FFT bins, we can increase 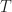 and it will be closer to an integer number of bins, as you suggest. But further increases may find it farther away again. If we look at
and it will be closer to an integer number of bins, as you suggest. But further increases may find it farther away again. If we look at  for a variety of
for a variety of 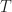 we get:
we get:
1024 51.2
2048 102.4
4096 204.8
… 409.6
… 819.2
… 1638.4
… 3276.8
… 6553.6
… 13107.2
… 26214.4
2^20 52428.8
So whether the frequency is close to an integer number of bins depends on the number of bins, and it doesn’t converge.
is close to an integer number of bins depends on the number of bins, and it doesn’t converge.
What is important is whether the accuracy of the representation of in terms of some integer number of FFT bins is small or larger relative to the inherent cycle-frequency resolution of the measurement, which is about
in terms of some integer number of FFT bins is small or larger relative to the inherent cycle-frequency resolution of the measurement, which is about 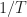 . The resolution of the measurement doesn’t change when we add zeros–we are just interpolating by zero padding. But by doing that interpolation, we allow the approximation of
. The resolution of the measurement doesn’t change when we add zeros–we are just interpolating by zero padding. But by doing that interpolation, we allow the approximation of  by an integer number of FFT bins to be more accurate, yet we do not have the problem of finer resolution that we would have if we increased the data length. So we get more accurate results with the same data.
by an integer number of FFT bins to be more accurate, yet we do not have the problem of finer resolution that we would have if we increased the data length. So we get more accurate results with the same data.
Moreover, increasing the data-block length to better represent one cycle frequency can result in a worse representation for another cycle frequency exhibited by the data. Zero-padding helps them all, or at least does no harm (if, say the cycle frequencies really are of the form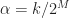 ).
).
Here is my offered evidence. (This was worth doing because I think we all struggle with this problem in the CSP community.) Sticking with our old friend the rectangular-pulse BPSK signal with bit rate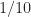 , carrier offset of
, carrier offset of  , unit power, and noise with
, unit power, and noise with 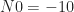 dB, we can plot the peak spectral correlation and spectral coherence magnitudes for a particular implementation of the FSM and a variety of block lengths
dB, we can plot the peak spectral correlation and spectral coherence magnitudes for a particular implementation of the FSM and a variety of block lengths 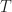 . First the spectral correlation:
. First the spectral correlation:
Next the coherence:
Notice that the cycle frequency of is unaffected by either zero padding. That is because that cycle frequency is always perfectly represented by an integer number of FFT bins. The others are affected though.
is unaffected by either zero padding. That is because that cycle frequency is always perfectly represented by an integer number of FFT bins. The others are affected though.
What do you say?
Thanks for the detailed response, Chad! I think you have some entire posts that are shorter…
Question on the coherence calculation – are you using the same FSM with the same zero-padding factor to compute the PSD and then the coherence for each case? It seems that the coherence values have higher variance than the SCF values themselves, though that might be deceptive plot scaling.
Your response spurred me to go back and improve my understanding of spectral and cycle frequency resolution (and temporal resolution, though my intuition is still terrible on what it means).
For my immediate purposes, I can select my data record lengths fairly arbitrarily, though I now (somewhat) better understand your comment about longer data records giving rise to higher cycle-frequency resolution (which has its own challenges).
I’m still wrapping my head around the fact that the FSM and the TSM both have approximately the same cycle frequency resolution. In your posts on resolution, you tended to focus on the FSM, which I think I (now) have a good handle on. I’m not clear on why the TSM has the cycle frequency resolution that it does. It “feels” like it should have a coarser cycle frequency resolution.
I’m also a little confused about the TSM relative to our zero-padding discussion, since the TSM (by definition) has far fewer FFT bins than the FSM, and thus ideal alpha/2 shifts will generally be further away from exact integers. However, zero-padding the entire signal wouldn’t help anything with the TSM, though I guess you could zero-pad each block. Not sure that that even makes sense though, as it wouldn’t? change the cycle frequency resolution relative to just increasing the block length.
Trying to explore the implications of and need for zero-padding – I tried to relate zero-padding to your post on the resolution product (https://cyclostationary.blog/2016/01/08/scf-estimate-quality-the-resolution-product/).
Let’s say we have a signal with N samples (in normalized units, I believe its temporal resolution is thus T=N). The spectral resolution, for the FSM, is then the length of the smoothing window, g, divided by N. And the resolution product then equals len(g)/N * N = len(g).
If we zero-pad the signal, I’m guessing that since zero-padding in time is like interpolating in frequency, then the spectral resolution is still just equal to len(g)/N. Or should it be len(g) / (N + num_zeros)? If the latter case, then is it appropriate to increase the length of g to maintain the same ratio as len(g)/N? Otherwise, the resolution product would shrink with the additional zero-padding, increasing the variance of the SCF estimate.
Lastly, why not just stick with shorter FFTs and interpolate the result in the frequency domain onto the finer grid? Seems like that could save a good bit of computation. The FFT is O( N log(N) ), while interpolation is just O(N). Perhaps better yet, why not just interpolate to the frequency points needed for the SCF calculation rather than do integer shifts of the data?
Yes.
Yes, the FFTs are typically quite short in the TSM, say,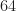 points or
points or 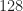 points. So the FFT bin size is wide, and many different cycle frequencies
points. So the FFT bin size is wide, and many different cycle frequencies 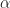 will map to the same set of FFT-shift-up and FFT-shift-down indices for each cyclic periodogram. So from that point of view, the resolution in
will map to the same set of FFT-shift-up and FFT-shift-down indices for each cyclic periodogram. So from that point of view, the resolution in 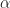 must be coarse. But remember there is another operation in the TSM that involves the cycle frequency
must be coarse. But remember there is another operation in the TSM that involves the cycle frequency 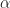 , and that is the cyclic-periodogram averaging operation, which involves the phase factor
, and that is the cyclic-periodogram averaging operation, which involves the phase factor 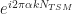 , where
, where 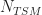 is that short TSM FFT length. That operation narrows the effective cycle-frequency resolution so that in the end, if you process
is that short TSM FFT length. That operation narrows the effective cycle-frequency resolution so that in the end, if you process 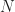 samples, you’ll get a cycle-frequency resolution of
samples, you’ll get a cycle-frequency resolution of 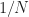 , just like in the FSM and SSCA. This is fairly easy to show mathematically, but I’ve not posted that to the CSP Blog yet.
, just like in the FSM and SSCA. This is fairly easy to show mathematically, but I’ve not posted that to the CSP Blog yet.
Yes, zero-padding in the TSM means zero-padding each short block prior to Fourier transformation, and you get about the same kind of improvement that you get with zero-padding in the FSM.
Well, after zero-padding, the frequency increments in the FFT are twice as narrow, so to keep the smoothing window width consistent in terms of Hz, you will have a window that is twice as many FFT bins in length as before:
No zero-padding: len(g) = G, total data samples = N, resolution product = (N) (G/N) = G
Zero-padding factor of two: len(g) = 2G, total data samples = N, resolution product = (N) (2G/2N) = G
I’m not sure I’m quite following this, but suppose you are doing the FSM for some cycle frequency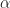 , and you are trying to estimate
, and you are trying to estimate  , and suppose further that the total number of processed samples is
, and suppose further that the total number of processed samples is 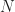 and
and 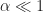 . Say,
. Say, 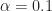 or
or 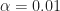 (this is a typical range). Then the extent of the function
(this is a typical range). Then the extent of the function  in spectral frequency
in spectral frequency 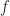 is large compared to the size of
is large compared to the size of 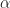 . That is, you have to estimate the spectral correlation function
. That is, you have to estimate the spectral correlation function  for many
for many 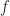 . So you need to “by hand” interpolate to find
. So you need to “by hand” interpolate to find 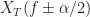 for a lot of
for a lot of 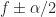 . Doing the zero-padding gets all of those at once. If you had one
. Doing the zero-padding gets all of those at once. If you had one 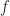 and one
and one 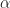 , then you are doing a point estimate of the spectral correlation function, and I think the FSM and TSM are overkill–they are meant to efficiently estimate the function-of-frequency
, then you are doing a point estimate of the spectral correlation function, and I think the FSM and TSM are overkill–they are meant to efficiently estimate the function-of-frequency  . Am I following you?
. Am I following you?
That clears up my thinking on most of the points; thanks!
Regarding the interpolation, let me try to explain my thinking a bit more.
As you suggest, let’s consider a signal x(n) with N samples.
We can get X(f) by taking the FFT of x, which requires O( N log(N) ) operations.
Let’s also zero-pad x(n) with P zeros to give x_pad(n) with M samples (M = N + P). Taking the FFT gives X_pad(f), which requires O( M log(M) ) operations.
To estimate S_x^alpha(f) with the FSM, we perform two shift operations on X_pad(f) to approximate X(f +/- alpha/2), and then multiply and smooth. This takes two sets of operations that are each O(M) (assuming the shifts are achieved through artistic indexing and thus essentially zero operations).
So, with zero-padding, it requires something like O( M (2 + log(M)) ) operations, and none of the resolutions are changed, though the accuracy of the cycle frequency is improved.
Alternatively, we could interpolate X(f) onto two frequency grids given by f +/- alpha/2 (e.g. using ‘interp1()’ in Matlab/Octave or NumPy’s interp() function) and multiply the result and smooth. This corresponds to four sets of operations that are each O(N).
With frequency-domain interpolation instead of zero-padding in time, we need O( N (4 + log(N)) ). And I believe all the resolutions would be the same, while achieving near-perfect accuracy of the cycle frequency. (And having fewer data points.)
I’m playing fast and loose with big-O notation here, but if P = N, then zero-padding takes O( 2N (2 + log(2N)) ) = O( 2N (3 + log(N)) ), while interpolation takes O( N (4 + log(N)) ).
In other words, for zero-padding by a factor of two, interpolation as I describe it _might_ save you a factor of two in number of operations. (Big-O notation was never meant to be used as precisely as I used it above, and it’s really going to come down to which FFT and interpolation implementations you use and exactly how many operations they require.)
So – interpolation may be more competitive for zero-padding by larger factors, and you could probably save a bit of computation for larger alpha values that result in substantial shrinking of the frequency domain. But it’s certainly not a big enough difference to matter until someone starts processing real data on a substantial scale.
Does that make sense? Do you agree that interpolation in the frequency domain would be at least as accurate as zero-padding in the time domain? Or am I missing something?
I think it can be, but there is no guarantee because not all interpolation methods are equivalent in terms of computational cost and outcome.
Here is an example illustrating that linear interpolation (using your suggestion: MATLAB’s interp1.m) does not improve the situation whereas zero-padding does:
The signal is a unit-amplitude complex-valued sine wave with a frequency that lies between two FFT bin centers: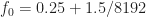 , where the FFT size is
, where the FFT size is 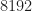 . Zero padding brings out the full strength of the tone in one bin, as expected because the frequency is exactly equal to an integer number of bins of width
. Zero padding brings out the full strength of the tone in one bin, as expected because the frequency is exactly equal to an integer number of bins of width 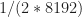 . But interpolating the complex-valued FFT using interp1.m results in a zero at that bin. Interpolating the magnitude of the FFT just replicates the value on either side of the bin for
. But interpolating the complex-valued FFT using interp1.m results in a zero at that bin. Interpolating the magnitude of the FFT just replicates the value on either side of the bin for 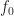 .
.
Do you buy this?
That does make sense. Can’t argue with the example you presented! 😉
I’d like to play around with it some, taking the process all the way through to estimating the SCF and tracking any effects to completely convince myself.
Fortunately or unfortunately, I’ve been caught up in working to better understand resolution and details like what you were explaining earlier in our conversation, applying various methods to the signals I currently care about.
For anyone following our discussion here, I’d also recommend looking through some related comments under the FFT Accumulation Method post. Several points there helped me to clarify my understanding of resolution and related matters.
Hi Dr. Spooner,
I’m sorry if this is a duplicate post. My first comment produced an error when I hit “Post Comment”. I’ll try again.
First, thank you *very* much for your blog. It is absolutely fantastic!
I feel like I’m understanding this particular post but I think there might be a small typo. When choosing two different shifts (i.e.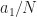 and
and 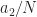 ) other than
) other than 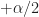 and
and 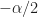 , what we really care about is the distance between
, what we really care about is the distance between 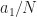 and
and 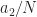 since we want that to be (exactly or very close to)
since we want that to be (exactly or very close to) 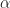 . If I’m understanding that accurately then I believe the statement “The idea is to choose the shifts
. If I’m understanding that accurately then I believe the statement “The idea is to choose the shifts 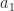 and
and 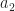 such that
such that 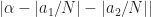 is minimized” should actually use the formula
is minimized” should actually use the formula 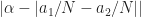 .
.
For a dumb example, if and
and  then
then 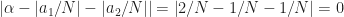 so the formula as given is minimized but the distance between
so the formula as given is minimized but the distance between 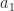 and
and 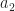 is 0 rather than
is 0 rather than 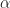 .
.
For another example, if and
and  and
and  then
then  but
but 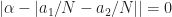 showing that the distance between
showing that the distance between 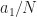 and
and 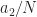 is equal to
is equal to 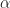 , producing the desired shift.
, producing the desired shift.
If I’ve missed something fundamental here, please let me know. Thanks again for this blog!
Thanks for checking out the CSP Blog, Willis, and for your generous compliments and great first comment. Very much appreciated!
Also, great job on using latex to format your symbols. I did edit your comment because enclosing the latex fragments between two dollar signs is not enough in WordPress–you must also include the keyword ‘latex’ just after the first dollar sign. If we do $\alpha$ we just see the latex code but if you put the word latex just after the left dollar sign, add a space, then the \alpha, you get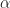 .
.
Thought-provoking comment! I was reading it late last evening and was thinking, ‘Uh-oh, messed up again.’ But looking at it this morning, I’m not so sure.
I think what we are focusing on is the distance between and
and 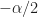 , because we have to take into account the negative sign in the second factor of the cyclic periodogram. The two shifts move the Fourier transform to the left by
, because we have to take into account the negative sign in the second factor of the cyclic periodogram. The two shifts move the Fourier transform to the left by  and to the right by
and to the right by  , for a total shift of
, for a total shift of 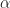 . It’s that negative sign that is causing some confusion here.
. It’s that negative sign that is causing some confusion here.
If we approximate the two shifts by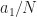 and
and 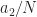 , the effective shift is related to
, the effective shift is related to 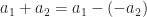 . I have to wade through a tangle of absolute value signs if I want to make sure I’m including negative cycle frequencies. I have slightly clarified the formula in the post, but I’m (so far) sticking with the basic formula you are grappling with.
. I have to wade through a tangle of absolute value signs if I want to make sure I’m including negative cycle frequencies. I have slightly clarified the formula in the post, but I’m (so far) sticking with the basic formula you are grappling with.
Yes, since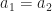 , the distance (difference) between
, the distance (difference) between 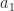 and
and 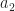 is zero, but that is not the same as the effective shift.
is zero, but that is not the same as the effective shift.  shifts the left factor in the cyclic periodogram one way by 1 FFT bin and the other factor by 1 the other way, for a total shift of two bins, which is the desired cycle frequency
shifts the left factor in the cyclic periodogram one way by 1 FFT bin and the other factor by 1 the other way, for a total shift of two bins, which is the desired cycle frequency 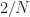 .
.
But choosing and
and  corresponds to a total shift in the cyclic periodogram of
corresponds to a total shift in the cyclic periodogram of 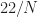 , which is not the desired cycle frequency. This is consistent with the fact that my formula is not minimized, as you point out, so those two
, which is not the desired cycle frequency. This is consistent with the fact that my formula is not minimized, as you point out, so those two 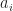 are not good candidates for
are not good candidates for  .
.
It gets a little more complicated (and annoying) when you consider the conjugate cyclic periodogram and conjugate spectral correlation function.
Buying it?
Hi Again Chad,
I have successfully implemented the FSM using some of the code people have posted, in particular for the frequency shift, the time domain shift is working well:
alpha=0.1
x1=y_of_t.*exp(-1i*2*pi*alpha/2.*[1:length(y_of_t)])
x2=y_of_t.*exp(1i*2*pi*alpha/2.*[1:length(y_of_t)])
X1=fftshift(fft(x1))
X2=fftshift(fft(x2))
S=X1.*conj(X2);
S=S/length(S);
s=rectwin(164)*(1/164)
f=conv(S,s)
freq=(-length(f)/2+1:length(f)/2)/(length(f));
plot(freq,abs(f))
Using BPSK 40,000 length signal. My question is, how can I perform the frequency shift in the frequency domain using equation (8) or (10)? My attempt was as follows:
Assuming a sampling rate of 1 MHz, left me with a bit rate of 100 kHz and that carrier frequency of 50 kHz, using your calculation from previous post this would get me alpha = 100 kHz for the first cyclic frequency or 0.1 normalised. I used straight fft on the 40k samples to calculate nfft=40000, fs=1 M, therefore frequency res = 25 Hz.
So to achieve alpha = 100 kHz I would need to move signal one to the right 4000 bins and signal two to the left 4000 bins. I chose to move signal 2 down 8000 bins instead and cut off the overlap at the end. But this does not produce the same result as the first code.
shift=-8000
x1=y_of_t
x2=circshift(y_of_t,shift)
X1=fftshift(fft(x1))
X2=fftshift(fft(x2))
S=X1.*conj(X2);
S=S/length(S);
s=rectwin(164)*(1/164)
f=conv(S,s)
freq=(-length(f)/2+1:length(f)/2)/(length(f));
plot(freq,abs(f))
Love the progress!
I confirm that the first code snippet produces a good estimate of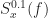 for the rectangular-pulse BPSK signal.
for the rectangular-pulse BPSK signal.
Regarding the second snippet, where you attempt to implement the shift in the frequency domain, you are actually still shifting things in the time domain:
shift=-8000
x1=y_of_t
x2=circshift(y_of_t,shift)
So the rest of that snippet then computes an estimate of the cross spectral density between y_of_t and a delayed (by 8000 samples) version of y_of_t.
The non-conjugate cyclic periodogram is
so that you have to apply the shifts of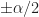 after you compute the Fourier transform (using fft.m)
after you compute the Fourier transform (using fft.m) 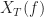 .
.
Thanks Chad,
A rookie mistake… I dunno how I missed that. It works now.
I make three rookie mistakes before I finish my morning coffee most days!